Question Number 154456 by puissant last updated on 18/Sep/21
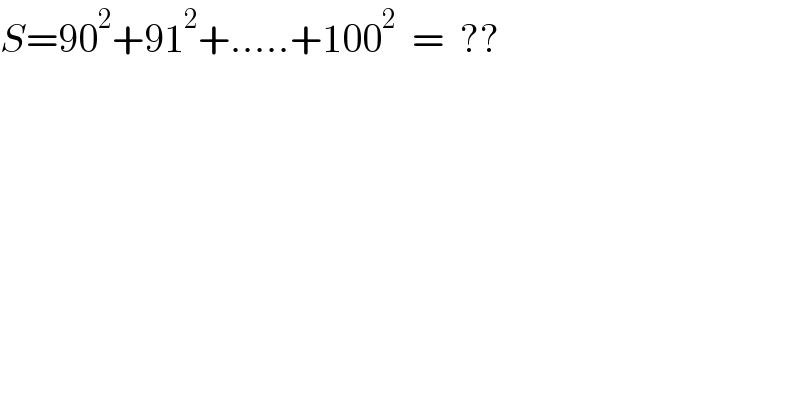
$${S}=\mathrm{90}^{\mathrm{2}} +\mathrm{91}^{\mathrm{2}} +…..+\mathrm{100}^{\mathrm{2}} \:\:=\:\:?? \\ $$
Commented by Rasheed.Sindhi last updated on 18/Sep/21
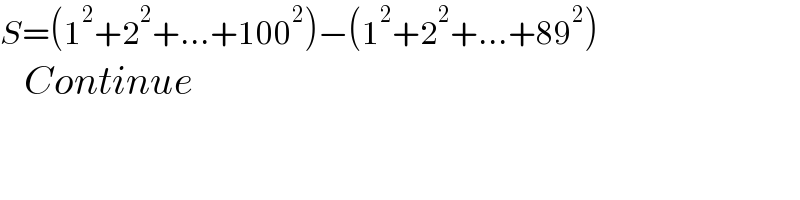
$${S}=\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +…+\mathrm{100}^{\mathrm{2}} \right)−\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +…+\mathrm{89}^{\mathrm{2}} \right) \\ $$$$\:\:\:{Continue} \\ $$
Commented by puissant last updated on 18/Sep/21

$${Thank}\:{you} \\ $$
Answered by amin96 last updated on 18/Sep/21
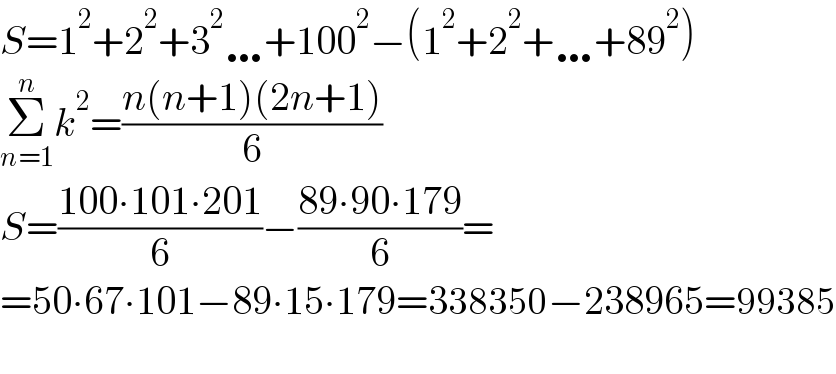
$${S}=\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} \ldots+\mathrm{100}^{\mathrm{2}} −\left(\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} +\ldots+\mathrm{89}^{\mathrm{2}} \right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} =\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}} \\ $$$${S}=\frac{\mathrm{100}\centerdot\mathrm{101}\centerdot\mathrm{201}}{\mathrm{6}}−\frac{\mathrm{89}\centerdot\mathrm{90}\centerdot\mathrm{179}}{\mathrm{6}}= \\ $$$$=\mathrm{50}\centerdot\mathrm{67}\centerdot\mathrm{101}−\mathrm{89}\centerdot\mathrm{15}\centerdot\mathrm{179}=\mathrm{338350}−\mathrm{238965}=\mathrm{99385} \\ $$$$ \\ $$
Commented by puissant last updated on 18/Sep/21

$${Thank}\:{you} \\ $$
