Menu Close

S-k-1-p-k-2-e-k-Find-S-

Tinku Tara 0 Comments
Pin




Question Number 147222 by alcohol last updated on 19/Jul/21
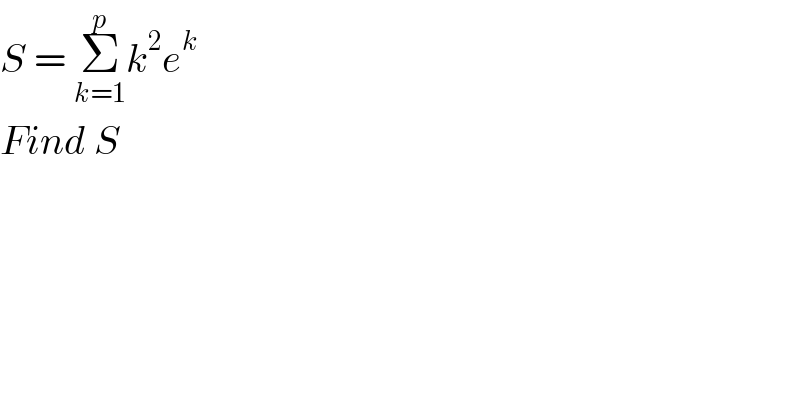
S = Σ_(k=1) ^p k^2 e^k Find S
$${S}\:=\:\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}{k}^{\mathrm{2}} {e}^{{k}} \\ $$$${Find}\:{S} \\ $$
Answered by mindispower last updated on 19/Jul/21
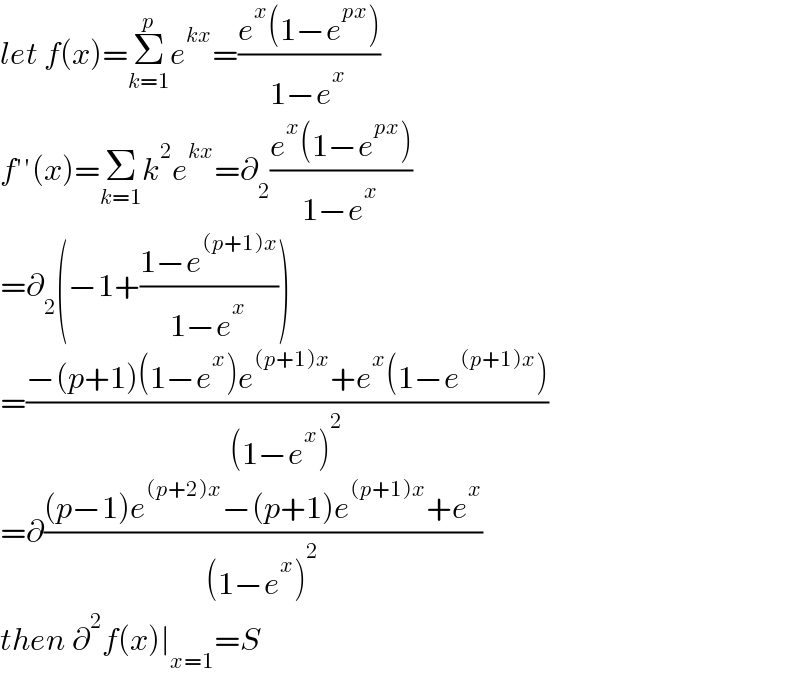
let f(x)=Σ_(k=1) ^p e^(kx) =((e^x (1−e^(px) ))/(1−e^x )) f′′(x)=Σ_(k=1) k^2 e^(kx) =∂_2 ((e^x (1−e^(px) ))/(1−e^x )) =∂_2 (−1+((1−e^((p+1)x) )/(1−e^x ))) =((−(p+1)(1−e^x )e^((p+1)x) +e^x (1−e^((p+1)x) ))/((1−e^x )^2 )) =∂(((p−1)e^((p+2)x) −(p+1)e^((p+1)x) +e^x )/((1−e^x )^2 )) then ∂^2 f(x)∣_(x=1) =S
$${let}\:{f}\left({x}\right)=\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}{e}^{{kx}} =\frac{{e}^{{x}} \left(\mathrm{1}−{e}^{{px}} \right)}{\mathrm{1}−{e}^{{x}} } \\ $$$${f}''\left({x}\right)=\underset{{k}=\mathrm{1}} {\sum}{k}^{\mathrm{2}} {e}^{{kx}} =\partial_{\mathrm{2}} \frac{{e}^{{x}} \left(\mathrm{1}−{e}^{{px}} \right)}{\mathrm{1}−{e}^{{x}} } \\ $$$$=\partial_{\mathrm{2}} \left(−\mathrm{1}+\frac{\mathrm{1}−{e}^{\left({p}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{x}} }\right) \\ $$$$=\frac{−\left({p}+\mathrm{1}\right)\left(\mathrm{1}−{e}^{{x}} \right){e}^{\left({p}+\mathrm{1}\right){x}} +{e}^{{x}} \left(\mathrm{1}−{e}^{\left({p}+\mathrm{1}\right){x}} \right)}{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$$=\partial\frac{\left({p}−\mathrm{1}\right){e}^{\left({p}+\mathrm{2}\right){x}} −\left({p}+\mathrm{1}\right){e}^{\left({p}+\mathrm{1}\right){x}} +{e}^{{x}} }{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} } \\ $$$${then}\:\partial^{\mathrm{2}} {f}\left({x}\right)\mid_{{x}=\mathrm{1}} ={S} \\ $$
Answered by Olaf_Thorendsen last updated on 19/Jul/21
S = Σ_(k=1) ^p k^2 e^k Let f(x) = Σ_(k=1) ^p e^(kx) = e^x ((1−e^(px) )/(1−e^x )) f′(x) = Σ_(k=1) ^p ke^(kx) = (d/dx)(e^x ((1−e^(kx) )/(1−e^x ))) f′′(x) = Σ_(k=1) ^p k^2 e^(kx) = (d^2 /dx^2 )(e^x ((1−e^(kx) )/(1−e^x ))) ⇒ S = f′′(1) = (d^2 /dx^2 )(e^x ((1−e^(kx) )/(1−e^x )))_(x=1) But the calculous of the second derivarive is fastidious.
$$\mathrm{S}\:=\:\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}{k}^{\mathrm{2}} {e}^{{k}} \\ $$$$\mathrm{Let}\:{f}\left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}{e}^{{kx}} \:=\:{e}^{{x}} \frac{\mathrm{1}−{e}^{{px}} }{\mathrm{1}−{e}^{{x}} } \\ $$$${f}'\left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}{ke}^{{kx}} \:=\:\frac{{d}}{{dx}}\left({e}^{{x}} \frac{\mathrm{1}−{e}^{{kx}} }{\mathrm{1}−{e}^{{x}} }\right) \\ $$$${f}''\left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{p}} {\sum}}{k}^{\mathrm{2}} {e}^{{kx}} \:=\:\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left({e}^{{x}} \frac{\mathrm{1}−{e}^{{kx}} }{\mathrm{1}−{e}^{{x}} }\right) \\ $$$$\Rightarrow\:\mathrm{S}\:=\:{f}''\left(\mathrm{1}\right)\:=\:\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left({e}^{{x}} \frac{\mathrm{1}−{e}^{{kx}} }{\mathrm{1}−{e}^{{x}} }\right)_{{x}=\mathrm{1}} \\ $$$$\mathrm{But}\:\mathrm{the}\:\mathrm{calculous}\:\mathrm{of}\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{derivarive}\:\mathrm{is}\:\mathrm{fastidious}. \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 20/Jul/21
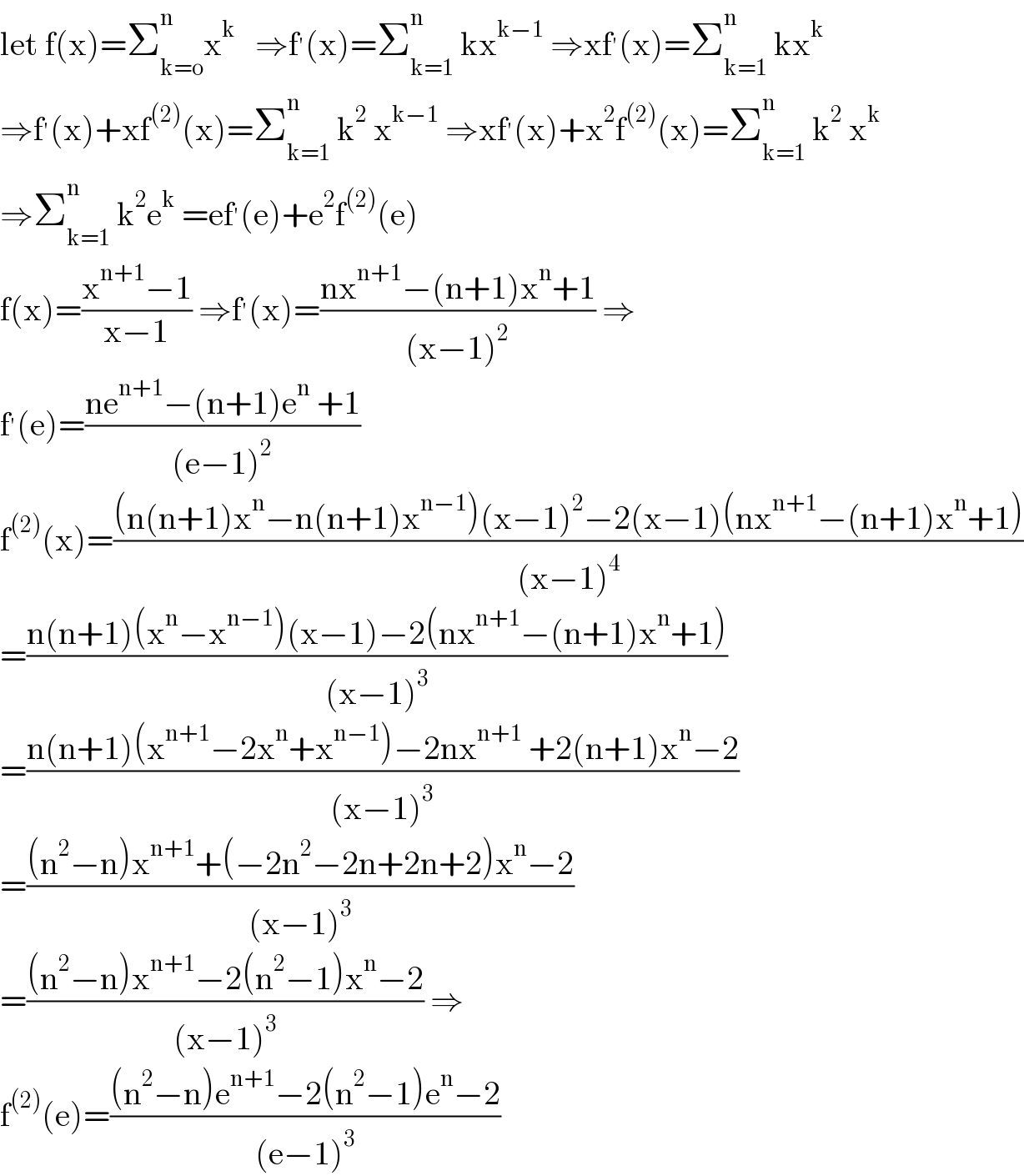
let f(x)=Σ_(k=o) ^n x^k ⇒f^′ (x)=Σ_(k=1) ^n kx^(k−1) ⇒xf^′ (x)=Σ_(k=1) ^n kx^k ⇒f^′ (x)+xf^((2)) (x)=Σ_(k=1) ^n k^2 x^(k−1) ⇒xf^′ (x)+x^2 f^((2)) (x)=Σ_(k=1) ^n k^2 x^k ⇒Σ_(k=1) ^n k^2 e^k =ef^′ (e)+e^2 f^((2)) (e) f(x)=((x^(n+1) −1)/(x−1)) ⇒f^′ (x)=((nx^(n+1) −(n+1)x^n +1)/((x−1)^2 )) ⇒ f^′ (e)=((ne^(n+1) −(n+1)e^n +1)/((e−1)^2 )) f^((2)) (x)=(((n(n+1)x^n −n(n+1)x^(n−1) )(x−1)^2 −2(x−1)(nx^(n+1) −(n+1)x^n +1))/((x−1)^4 )) =((n(n+1)(x^n −x^(n−1) )(x−1)−2(nx^(n+1) −(n+1)x^n +1))/((x−1)^3 )) =((n(n+1)(x^(n+1) −2x^n +x^(n−1) )−2nx^(n+1) +2(n+1)x^n −2)/((x−1)^3 )) =(((n^2 −n)x^(n+1) +(−2n^2 −2n+2n+2)x^n −2)/((x−1)^3 )) =(((n^2 −n)x^(n+1) −2(n^2 −1)x^n −2)/((x−1)^3 )) ⇒ f^((2)) (e)=(((n^2 −n)e^(n+1) −2(n^2 −1)e^n −2)/((e−1)^3 ))
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{o}} ^{\mathrm{n}} \mathrm{x}^{\mathrm{k}} \:\:\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}−\mathrm{1}} \:\Rightarrow\mathrm{xf}^{'} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{kx}^{\mathrm{k}} \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)+\mathrm{xf}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \:\mathrm{x}^{\mathrm{k}−\mathrm{1}} \:\Rightarrow\mathrm{xf}^{'} \left(\mathrm{x}\right)+\mathrm{x}^{\mathrm{2}} \mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \:\mathrm{x}^{\mathrm{k}} \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \mathrm{e}^{\mathrm{k}} \:=\mathrm{ef}^{'} \left(\mathrm{e}\right)+\mathrm{e}^{\mathrm{2}} \mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{e}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{x}−\mathrm{1}}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} +\mathrm{1}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{e}\right)=\frac{\mathrm{ne}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{e}^{\mathrm{n}} \:+\mathrm{1}}{\left(\mathrm{e}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\frac{\left(\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} −\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} +\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{n}} −\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)\left(\mathrm{x}−\mathrm{1}\right)−\mathrm{2}\left(\mathrm{nx}^{\mathrm{n}+\mathrm{1}} −\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} +\mathrm{1}\right)}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{2x}^{\mathrm{n}} +\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)−\mathrm{2nx}^{\mathrm{n}+\mathrm{1}} \:+\mathrm{2}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} −\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{n}^{\mathrm{2}} −\mathrm{n}\right)\mathrm{x}^{\mathrm{n}+\mathrm{1}} +\left(−\mathrm{2n}^{\mathrm{2}} −\mathrm{2n}+\mathrm{2n}+\mathrm{2}\right)\mathrm{x}^{\mathrm{n}} −\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{n}^{\mathrm{2}} −\mathrm{n}\right)\mathrm{x}^{\mathrm{n}+\mathrm{1}} −\mathrm{2}\left(\mathrm{n}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{x}^{\mathrm{n}} −\mathrm{2}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{e}\right)=\frac{\left(\mathrm{n}^{\mathrm{2}} −\mathrm{n}\right)\mathrm{e}^{\mathrm{n}+\mathrm{1}} −\mathrm{2}\left(\mathrm{n}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{e}^{\mathrm{n}} −\mathrm{2}}{\left(\mathrm{e}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *