Question Number 160604 by cortano last updated on 03/Dec/21
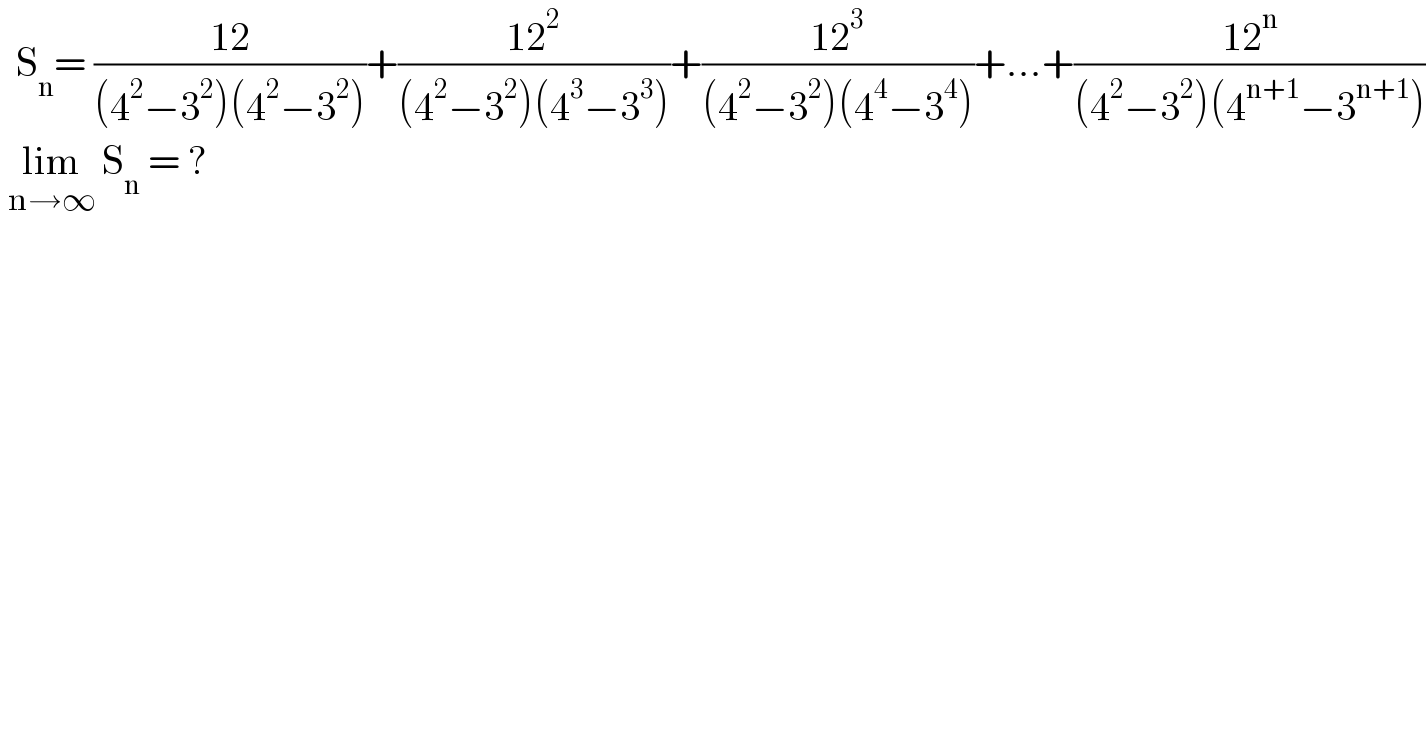
$$\:\:\mathrm{S}_{\mathrm{n}} =\:\frac{\mathrm{12}}{\left(\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)}+\frac{\mathrm{12}^{\mathrm{2}} }{\left(\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{3}} −\mathrm{3}^{\mathrm{3}} \right)}+\frac{\mathrm{12}^{\mathrm{3}} }{\left(\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{4}} −\mathrm{3}^{\mathrm{4}} \right)}+…+\frac{\mathrm{12}^{\mathrm{n}} }{\left(\mathrm{4}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} \right)\left(\mathrm{4}^{\mathrm{n}+\mathrm{1}} −\mathrm{3}^{\mathrm{n}+\mathrm{1}} \right)} \\ $$$$\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{S}_{\mathrm{n}} \:=\:? \\ $$
