S-n-4-n-1-1-n-2-

Question Number 127344 by bobhans last updated on 29/Dec/20

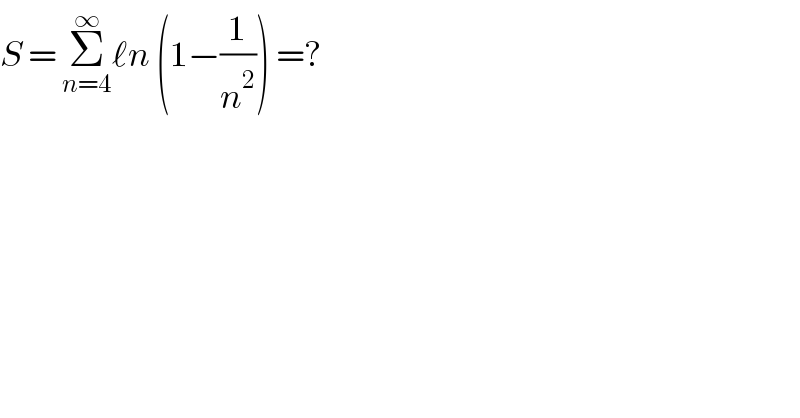
$${S}\:=\:\underset{{n}=\mathrm{4}} {\overset{\infty} {\sum}}\ell{n}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:=?\: \\ $$

Answered by liberty last updated on 29/Dec/20

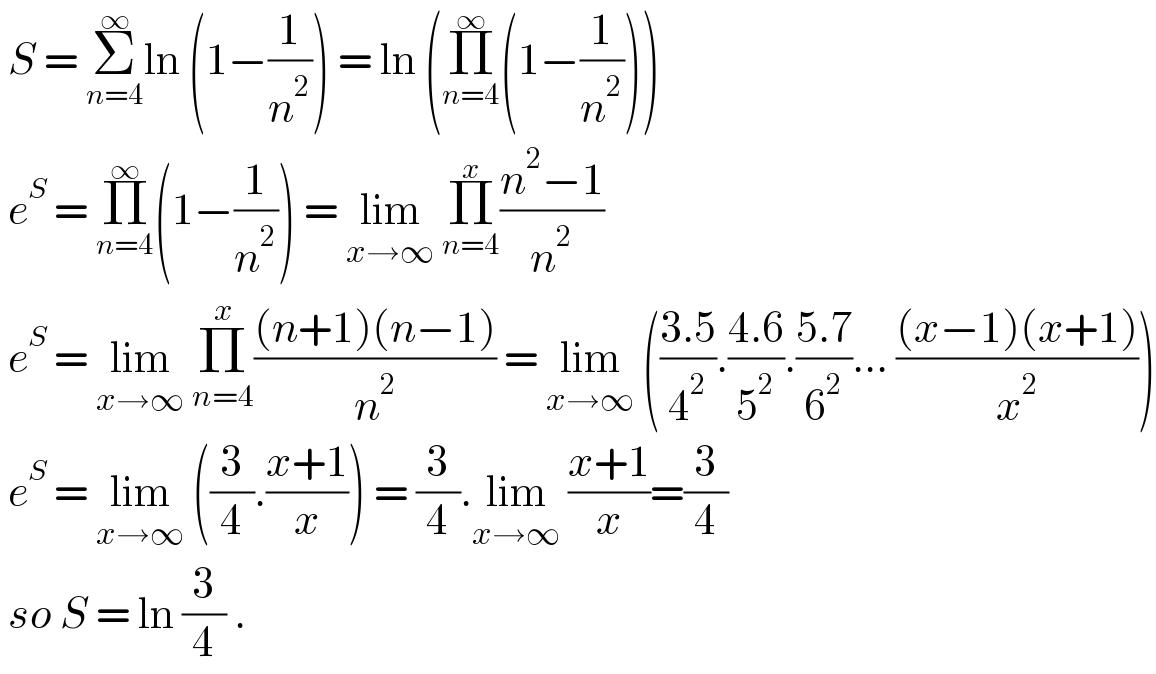
S = Σ_(n=4) ^∞ ln (1−(1/n^2 )) = ln (Π_(n=4) ^∞ (1−(1/n^2 ))) e^S = Π_(n=4) ^∞ (1−(1/n^2 )) = lim_(x→∞) Π_(n=4) ^x ((n^2 −1)/n^2 ) e^S = lim_(x→∞) Π_(n=4) ^x (((n+1)(n−1))/n^2 ) = lim_(x→∞) (((3.5)/4^2 ).((4.6)/5^2 ).((5.7)/6^2 )... (((x−1)(x+1))/x^2 )) e^S = lim_(x→∞) ((3/4).((x+1)/x)) = (3/4).lim_(x→∞) ((x+1)/x)=(3/4) so S = ln (3/4) .

$$\:{S}\:=\:\underset{{n}=\mathrm{4}} {\overset{\infty} {\sum}}\mathrm{ln}\:\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:=\:\mathrm{ln}\:\left(\underset{{n}=\mathrm{4}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\right) \\ $$$$\:{e}^{{S}} \:=\:\underset{{n}=\mathrm{4}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\underset{{n}=\mathrm{4}} {\overset{{x}} {\prod}}\frac{{n}^{\mathrm{2}} −\mathrm{1}}{{n}^{\mathrm{2}} }\: \\ $$$$\:{e}^{{S}} \:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\underset{{n}=\mathrm{4}} {\overset{{x}} {\prod}}\frac{\left({n}+\mathrm{1}\right)\left({n}−\mathrm{1}\right)}{{n}^{\mathrm{2}} }\:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{3}.\mathrm{5}}{\mathrm{4}^{\mathrm{2}} }.\frac{\mathrm{4}.\mathrm{6}}{\mathrm{5}^{\mathrm{2}} }.\frac{\mathrm{5}.\mathrm{7}}{\mathrm{6}^{\mathrm{2}} }…\:\frac{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} }\right) \\ $$$$\:{e}^{{S}} \:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{3}}{\mathrm{4}}.\frac{{x}+\mathrm{1}}{{x}}\right)\:=\:\frac{\mathrm{3}}{\mathrm{4}}.\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}+\mathrm{1}}{{x}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\:{so}\:{S}\:=\:\mathrm{ln}\:\frac{\mathrm{3}}{\mathrm{4}}\:. \\ $$

Answered by mindispower last updated on 29/Dec/20

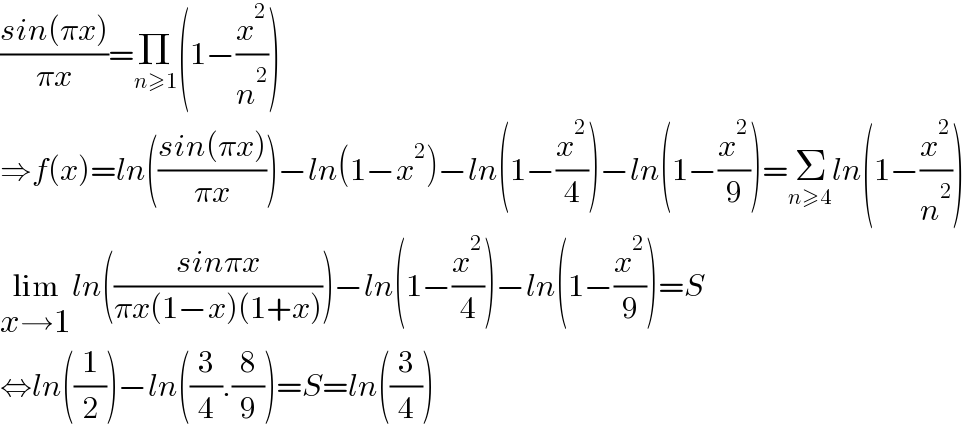
((sin(πx))/(πx))=Π_(n≥1) (1−(x^2 /n^2 )) ⇒f(x)=ln(((sin(πx))/(πx)))−ln(1−x^2 )−ln(1−(x^2 /4))−ln(1−(x^2 /9))=Σ_(n≥4) ln(1−(x^2 /n^2 )) lim_(x→1) ln(((sinπx)/(πx(1−x)(1+x))))−ln(1−(x^2 /4))−ln(1−(x^2 /9))=S ⇔ln((1/2))−ln((3/4).(8/9))=S=ln((3/4))

$$\frac{{sin}\left(\pi{x}\right)}{\pi{x}}=\underset{{n}\geqslant\mathrm{1}} {\prod}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{f}\left({x}\right)={ln}\left(\frac{{sin}\left(\pi{x}\right)}{\pi{x}}\right)−{ln}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)−{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right)−{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{9}}\right)=\underset{{n}\geqslant\mathrm{4}} {\sum}{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}{ln}\left(\frac{{sin}\pi{x}}{\pi{x}\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)}\right)−{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\right)−{ln}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{9}}\right)={S} \\ $$$$\Leftrightarrow{ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{ln}\left(\frac{\mathrm{3}}{\mathrm{4}}.\frac{\mathrm{8}}{\mathrm{9}}\right)={S}={ln}\left(\frac{\mathrm{3}}{\mathrm{4}}\right) \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply