Menu Close

S-n-k-1-1-4k-2-1-n-find-a-simpler-form-

Tinku Tara 0 Comments
Pin




Question Number 92925 by frc2crc last updated on 09/May/20
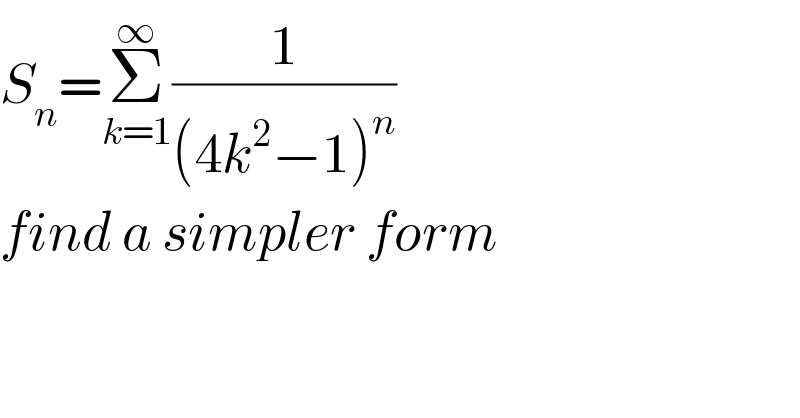
S_n =Σ_(k=1) ^∞ (1/((4k^2 −1)^n )) find a simpler form
$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}\right)^{{n}} } \\ $$$${find}\:{a}\:{simpler}\:{form} \\ $$
Commented by mr W last updated on 09/May/20
check your question please. Σ_(k=1) ^(n or ∞)
$${check}\:{your}\:{question}\:{please}. \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}\:{or}\:\infty} {\sum}} \\ $$
Commented by frc2crc last updated on 09/May/20
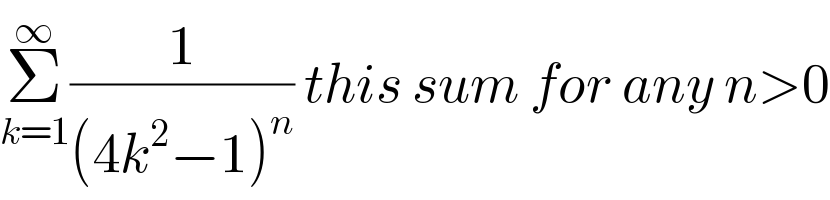
Σ_(k=1) ^∞ (1/((4k^2 −1)^n )) this sum for any n>0
$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}\right)^{{n}} }\:{this}\:{sum}\:{for}\:{any}\:{n}>\mathrm{0} \\ $$
Commented by prakash jain last updated on 09/May/20
series is convergent for n≥1. We can use limit comparion test. n=1 (1/(4k^2 −1))=(1/2)((1/(2k−1))−(1/(2k+1))) ⇒Σ_(k=1) ^∞ (1/(4k^2 −1))=(1/2) n=2 can be evaluated using known series expansion for π^2 . −−−−− I will check if a generic closed form formula is possible. It may exists using zeta function.
$$\mathrm{series}\:\mathrm{is}\:\mathrm{convergent}\:\mathrm{for}\:{n}\geqslant\mathrm{1}.\:\mathrm{We} \\ $$$$\mathrm{can}\:\mathrm{use}\:\mathrm{limit}\:\mathrm{comparion}\:\mathrm{test}. \\ $$$${n}=\mathrm{1} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}{k}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\right) \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{n}=\mathrm{2}\:\mathrm{can}\:\mathrm{be}\:\mathrm{evaluated}\:\mathrm{using} \\ $$$$\mathrm{known}\:\mathrm{series}\:\mathrm{expansion}\:\mathrm{for}\:\pi^{\mathrm{2}} . \\ $$$$−−−−− \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{check}\:\mathrm{if}\:\mathrm{a}\:\mathrm{generic}\:\mathrm{closed} \\ $$$$\mathrm{form}\:\mathrm{formula}\:\mathrm{is}\:\mathrm{possible}. \\ $$$$\mathrm{It}\:\mathrm{may}\:\mathrm{exists}\:\mathrm{using}\:\mathrm{zeta}\:\mathrm{function}. \\ $$$$ \\ $$
Commented by abdomathmax last updated on 10/May/20
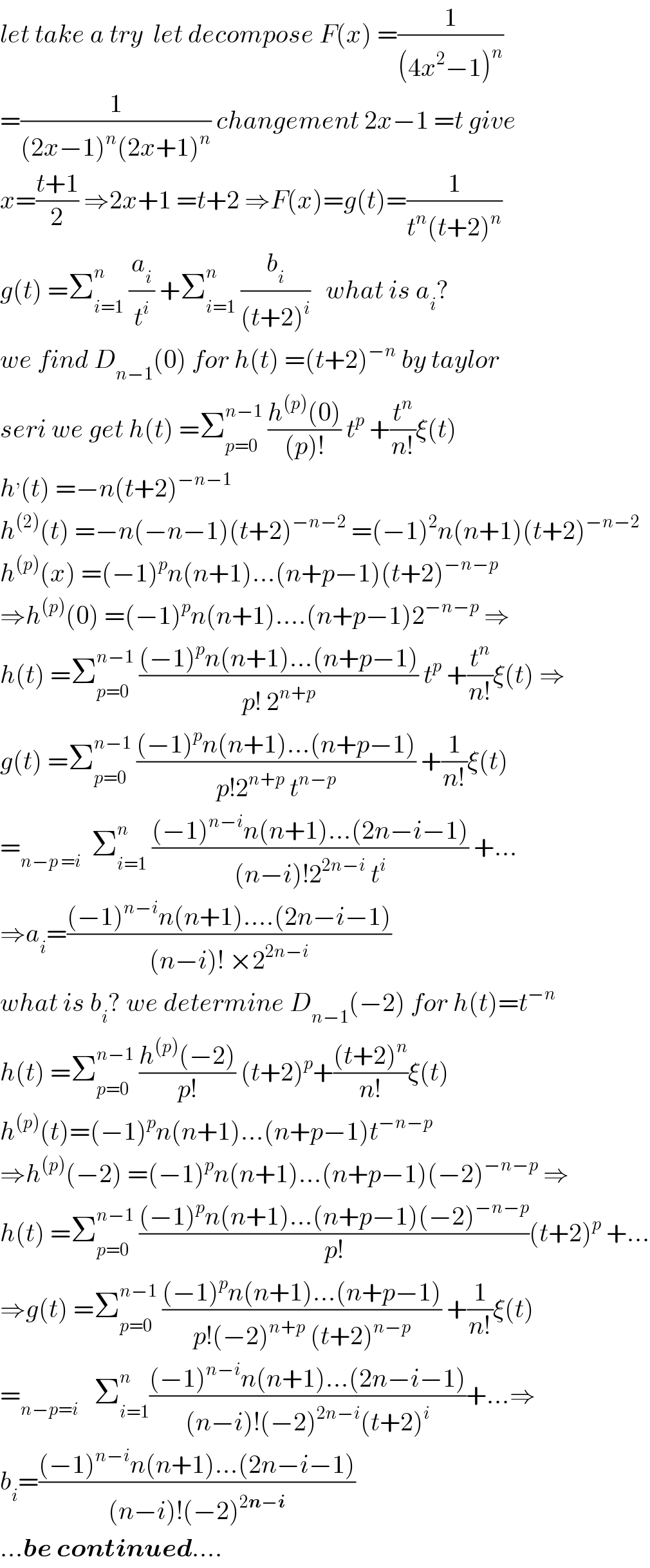
let take a try let decompose F(x) =(1/((4x^2 −1)^n )) =(1/((2x−1)^n (2x+1)^n )) changement 2x−1 =t give x=((t+1)/2) ⇒2x+1 =t+2 ⇒F(x)=g(t)=(1/(t^n (t+2)^n )) g(t) =Σ_(i=1) ^n (a_i /t^i ) +Σ_(i=1) ^n (b_i /((t+2)^i )) what is a_i ? we find D_(n−1) (0) for h(t) =(t+2)^(−n) by taylor seri we get h(t) =Σ_(p=0) ^(n−1) ((h^((p)) (0))/((p)!)) t^p +(t^n /(n!))ξ(t) h^, (t) =−n(t+2)^(−n−1) h^((2)) (t) =−n(−n−1)(t+2)^(−n−2) =(−1)^2 n(n+1)(t+2)^(−n−2) h^((p)) (x) =(−1)^p n(n+1)...(n+p−1)(t+2)^(−n−p) ⇒h^((p)) (0) =(−1)^p n(n+1)....(n+p−1)2^(−n−p) ⇒ h(t) =Σ_(p=0) ^(n−1) (((−1)^p n(n+1)...(n+p−1))/(p! 2^(n+p) )) t^p +(t^n /(n!))ξ(t) ⇒ g(t) =Σ_(p=0) ^(n−1) (((−1)^p n(n+1)...(n+p−1))/(p!2^(n+p) t^(n−p) )) +(1/(n!))ξ(t) =_(n−p =i) Σ_(i=1) ^n (((−1)^(n−i) n(n+1)...(2n−i−1))/((n−i)!2^(2n−i) t^i )) +... ⇒a_i =(((−1)^(n−i) n(n+1)....(2n−i−1))/((n−i)! ×2^(2n−i) )) what is b_i ? we determine D_(n−1) (−2) for h(t)=t^(−n) h(t) =Σ_(p=0) ^(n−1) ((h^((p)) (−2))/(p!)) (t+2)^p +(((t+2)^n )/(n!))ξ(t) h^((p)) (t)=(−1)^p n(n+1)...(n+p−1)t^(−n−p) ⇒h^((p)) (−2) =(−1)^p n(n+1)...(n+p−1)(−2)^(−n−p) ⇒ h(t) =Σ_(p=0) ^(n−1) (((−1)^p n(n+1)...(n+p−1)(−2)^(−n−p) )/(p!))(t+2)^p +... ⇒g(t) =Σ_(p=0) ^(n−1) (((−1)^p n(n+1)...(n+p−1))/(p!(−2)^(n+p) (t+2)^(n−p) )) +(1/(n!))ξ(t) =_(n−p=i) Σ_(i=1) ^n (((−1)^(n−i) n(n+1)...(2n−i−1))/((n−i)!(−2)^(2n−i) (t+2)^i ))+...⇒ b_i =(((−1)^(n−i) n(n+1)...(2n−i−1))/((n−i)!(−2)^(2n−i) )) ...be continued....
$${let}\:{take}\:{a}\:{try}\:\:{let}\:{decompose}\:{F}\left({x}\right)\:=\frac{\mathrm{1}}{\left(\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\right)^{{n}} } \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2}{x}−\mathrm{1}\right)^{{n}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{{n}} }\:{changement}\:\mathrm{2}{x}−\mathrm{1}\:={t}\:{give} \\ $$$${x}=\frac{{t}+\mathrm{1}}{\mathrm{2}}\:\Rightarrow\mathrm{2}{x}+\mathrm{1}\:={t}+\mathrm{2}\:\Rightarrow{F}\left({x}\right)={g}\left({t}\right)=\frac{\mathrm{1}}{{t}^{{n}} \left({t}+\mathrm{2}\right)^{{n}} } \\ $$$${g}\left({t}\right)\:=\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{{a}_{{i}} }{{t}^{{i}} }\:+\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{{b}_{{i}} }{\left({t}+\mathrm{2}\right)^{{i}} }\:\:\:{what}\:{is}\:{a}_{{i}} ? \\ $$$${we}\:{find}\:{D}_{{n}−\mathrm{1}} \left(\mathrm{0}\right)\:{for}\:{h}\left({t}\right)\:=\left({t}+\mathrm{2}\right)^{−{n}} \:{by}\:{taylor} \\ $$$${seri}\:{we}\:{get}\:{h}\left({t}\right)\:=\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{h}^{\left({p}\right)} \left(\mathrm{0}\right)}{\left({p}\right)!}\:{t}^{{p}} \:+\frac{{t}^{{n}} }{{n}!}\xi\left({t}\right) \\ $$$${h}^{,} \left({t}\right)\:=−{n}\left({t}+\mathrm{2}\right)^{−{n}−\mathrm{1}} \: \\ $$$${h}^{\left(\mathrm{2}\right)} \left({t}\right)\:=−{n}\left(−{n}−\mathrm{1}\right)\left({t}+\mathrm{2}\right)^{−{n}−\mathrm{2}} \:=\left(−\mathrm{1}\right)^{\mathrm{2}} {n}\left({n}+\mathrm{1}\right)\left({t}+\mathrm{2}\right)^{−{n}−\mathrm{2}} \\ $$$${h}^{\left({p}\right)} \left({x}\right)\:=\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)…\left({n}+{p}−\mathrm{1}\right)\left({t}+\mathrm{2}\right)^{−{n}−{p}} \\ $$$$\Rightarrow{h}^{\left({p}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)….\left({n}+{p}−\mathrm{1}\right)\mathrm{2}^{−{n}−{p}} \:\Rightarrow \\ $$$${h}\left({t}\right)\:=\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)…\left({n}+{p}−\mathrm{1}\right)}{{p}!\:\mathrm{2}^{{n}+{p}} }\:{t}^{{p}} \:+\frac{{t}^{{n}} }{{n}!}\xi\left({t}\right)\:\Rightarrow \\ $$$${g}\left({t}\right)\:=\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)…\left({n}+{p}−\mathrm{1}\right)}{{p}!\mathrm{2}^{{n}+{p}} \:{t}^{{n}−{p}} }\:+\frac{\mathrm{1}}{{n}!}\xi\left({t}\right) \\ $$$$=_{{n}−{p}\:={i}} \:\:\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\left(−\mathrm{1}\right)^{{n}−{i}} {n}\left({n}+\mathrm{1}\right)…\left(\mathrm{2}{n}−{i}−\mathrm{1}\right)}{\left({n}−{i}\right)!\mathrm{2}^{\mathrm{2}{n}−{i}} \:{t}^{{i}} }\:+… \\ $$$$\Rightarrow{a}_{{i}} =\frac{\left(−\mathrm{1}\right)^{{n}−{i}} {n}\left({n}+\mathrm{1}\right)….\left(\mathrm{2}{n}−{i}−\mathrm{1}\right)}{\left({n}−{i}\right)!\:×\mathrm{2}^{\mathrm{2}{n}−{i}} } \\ $$$${what}\:{is}\:{b}_{{i}} ?\:{we}\:{determine}\:{D}_{{n}−\mathrm{1}} \left(−\mathrm{2}\right)\:{for}\:{h}\left({t}\right)={t}^{−{n}} \\ $$$${h}\left({t}\right)\:=\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{{h}^{\left({p}\right)} \left(−\mathrm{2}\right)}{{p}!}\:\left({t}+\mathrm{2}\right)^{{p}} +\frac{\left({t}+\mathrm{2}\right)^{{n}} }{{n}!}\xi\left({t}\right) \\ $$$${h}^{\left({p}\right)} \left({t}\right)=\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)…\left({n}+{p}−\mathrm{1}\right){t}^{−{n}−{p}} \\ $$$$\Rightarrow{h}^{\left({p}\right)} \left(−\mathrm{2}\right)\:=\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)…\left({n}+{p}−\mathrm{1}\right)\left(−\mathrm{2}\right)^{−{n}−{p}} \:\Rightarrow \\ $$$${h}\left({t}\right)\:=\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)…\left({n}+{p}−\mathrm{1}\right)\left(−\mathrm{2}\right)^{−{n}−{p}} }{{p}!}\left({t}+\mathrm{2}\right)^{{p}} \:+… \\ $$$$\Rightarrow{g}\left({t}\right)\:=\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{{p}} {n}\left({n}+\mathrm{1}\right)…\left({n}+{p}−\mathrm{1}\right)}{{p}!\left(−\mathrm{2}\right)^{{n}+{p}} \:\left({t}+\mathrm{2}\right)^{{n}−{p}} }\:+\frac{\mathrm{1}}{{n}!}\xi\left({t}\right) \\ $$$$=_{{n}−{p}={i}} \:\:\:\sum_{{i}=\mathrm{1}} ^{{n}} \frac{\left(−\mathrm{1}\right)^{{n}−{i}} {n}\left({n}+\mathrm{1}\right)…\left(\mathrm{2}{n}−{i}−\mathrm{1}\right)}{\left({n}−{i}\right)!\left(−\mathrm{2}\right)^{\mathrm{2}{n}−{i}} \left({t}+\mathrm{2}\right)^{{i}} }+…\Rightarrow \\ $$$${b}_{{i}} =\frac{\left(−\mathrm{1}\right)^{{n}−{i}} {n}\left({n}+\mathrm{1}\right)…\left(\mathrm{2}{n}−{i}−\mathrm{1}\right)}{\left({n}−{i}\right)!\left(−\mathrm{2}\right)^{\mathrm{2}\boldsymbol{{n}}−\boldsymbol{{i}}} } \\ $$$$…\boldsymbol{{be}}\:\boldsymbol{{continued}}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *