Menu Close

S-n-k-1-n-1-k-k-2-k-4-lim-n-S-n-

Tinku Tara 0 Comments
Pin




Question Number 146307 by mnjuly1970 last updated on 12/Jul/21
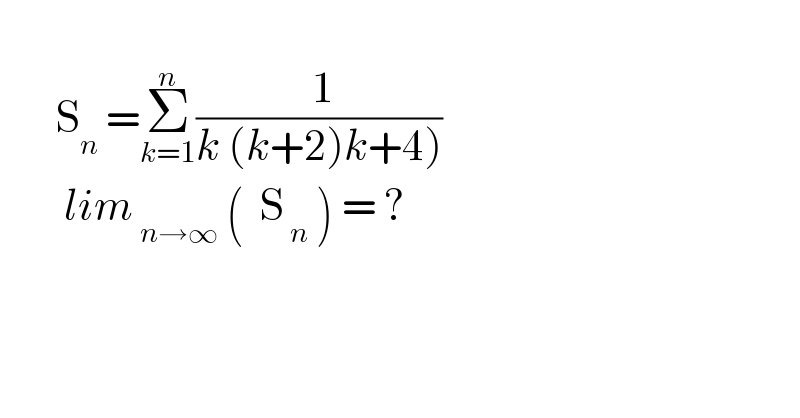
S_n =Σ_(k=1) ^n (( 1)/(k (k+2)k+4))) lim_( n→∞) ( S_( n) ) = ?
$$ \\ $$$$\:\:\:\:\:\:\:\mathrm{S}_{{n}} \:=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\:\mathrm{1}}{\left.{k}\:\left({k}+\mathrm{2}\right){k}+\mathrm{4}\right)} \\ $$$$\:\:\:\:\:\:\:\:{lim}_{\:{n}\rightarrow\infty} \:\left(\:\:\mathrm{S}_{\:{n}} \:\right)\:=\:? \\ $$
Answered by mathmax by abdo last updated on 12/Jul/21
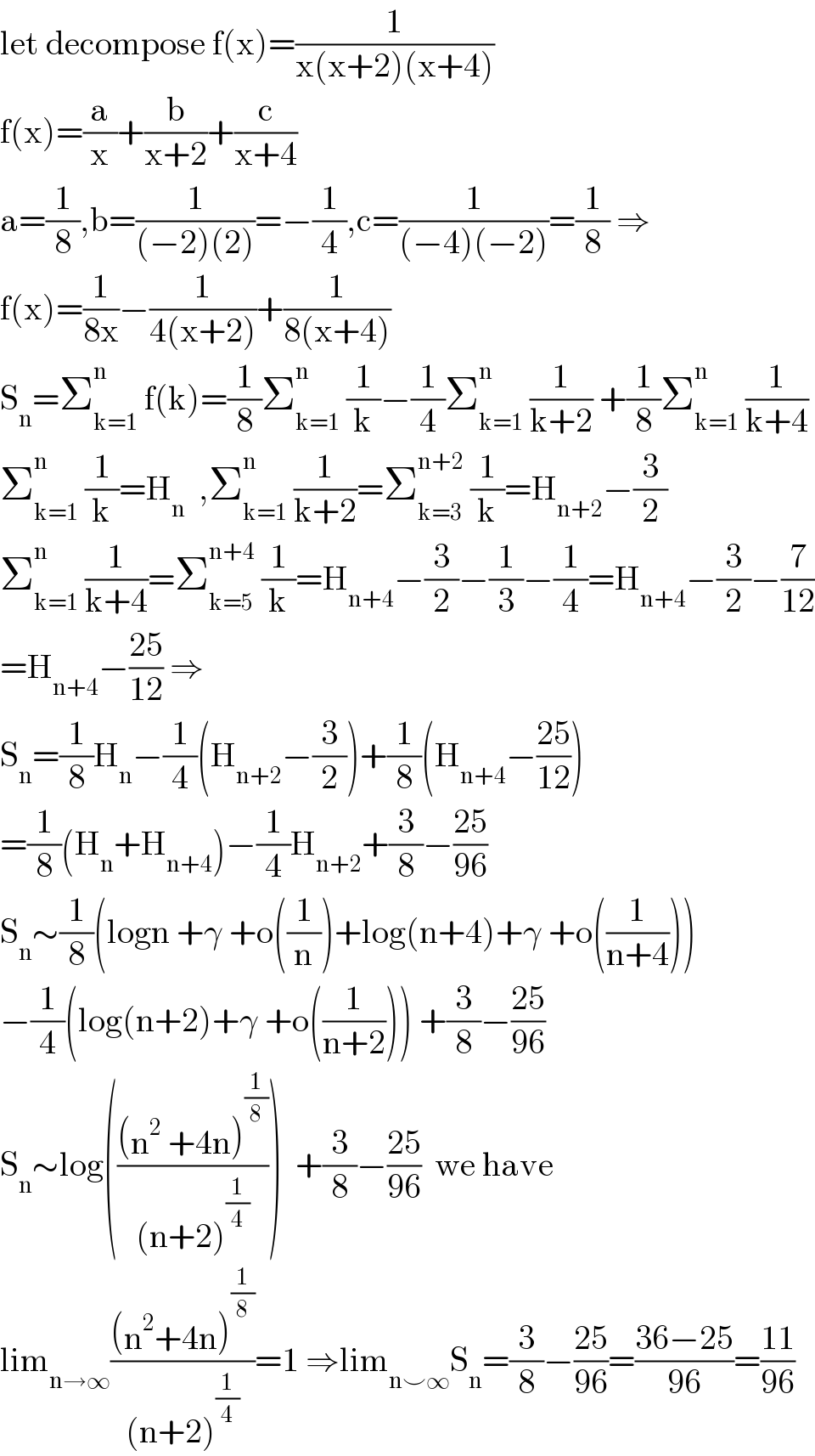
let decompose f(x)=(1/(x(x+2)(x+4))) f(x)=(a/x)+(b/(x+2))+(c/(x+4)) a=(1/8),b=(1/((−2)(2)))=−(1/4),c=(1/((−4)(−2)))=(1/8) ⇒ f(x)=(1/(8x))−(1/(4(x+2)))+(1/(8(x+4))) S_n =Σ_(k=1) ^n f(k)=(1/8)Σ_(k=1) ^n (1/k)−(1/4)Σ_(k=1) ^n (1/(k+2)) +(1/8)Σ_(k=1) ^n (1/(k+4)) Σ_(k=1) ^n (1/k)=H_n ,Σ_(k=1) ^n (1/(k+2))=Σ_(k=3) ^(n+2) (1/k)=H_(n+2) −(3/2) Σ_(k=1) ^n (1/(k+4))=Σ_(k=5) ^(n+4) (1/k)=H_(n+4) −(3/2)−(1/3)−(1/4)=H_(n+4) −(3/2)−(7/(12)) =H_(n+4) −((25)/(12)) ⇒ S_n =(1/8)H_n −(1/4)(H_(n+2) −(3/2))+(1/8)(H_(n+4) −((25)/(12))) =(1/8)(H_n +H_(n+4) )−(1/4)H_(n+2) +(3/8)−((25)/(96)) S_n ∼(1/8)(logn +γ +o((1/n))+log(n+4)+γ +o((1/(n+4)))) −(1/4)(log(n+2)+γ +o((1/(n+2)))) +(3/8)−((25)/(96)) S_n ∼log((((n^2 +4n)^(1/8) )/((n+2)^(1/4) ))) +(3/8)−((25)/(96)) we have lim_(n→∞) (((n^2 +4n)^(1/8) )/((n+2)^(1/4) ))=1 ⇒lim_(n⌣∞) S_n =(3/8)−((25)/(96))=((36−25)/(96))=((11)/(96))
$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{x}+\mathrm{4}\right)} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{a}}{\mathrm{x}}+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{2}}+\frac{\mathrm{c}}{\mathrm{x}+\mathrm{4}} \\ $$$$\mathrm{a}=\frac{\mathrm{1}}{\mathrm{8}},\mathrm{b}=\frac{\mathrm{1}}{\left(−\mathrm{2}\right)\left(\mathrm{2}\right)}=−\frac{\mathrm{1}}{\mathrm{4}},\mathrm{c}=\frac{\mathrm{1}}{\left(−\mathrm{4}\right)\left(−\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{8x}}−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{x}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{x}+\mathrm{4}\right)} \\ $$$$\mathrm{S}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{f}\left(\mathrm{k}\right)=\frac{\mathrm{1}}{\mathrm{8}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{4}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{4}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}}=\mathrm{H}_{\mathrm{n}} \:\:,\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{2}}=\sum_{\mathrm{k}=\mathrm{3}} ^{\mathrm{n}+\mathrm{2}} \:\frac{\mathrm{1}}{\mathrm{k}}=\mathrm{H}_{\mathrm{n}+\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\frac{\mathrm{1}}{\mathrm{k}+\mathrm{4}}=\sum_{\mathrm{k}=\mathrm{5}} ^{\mathrm{n}+\mathrm{4}} \:\frac{\mathrm{1}}{\mathrm{k}}=\mathrm{H}_{\mathrm{n}+\mathrm{4}} −\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}=\mathrm{H}_{\mathrm{n}+\mathrm{4}} −\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{7}}{\mathrm{12}} \\ $$$$=\mathrm{H}_{\mathrm{n}+\mathrm{4}} −\frac{\mathrm{25}}{\mathrm{12}}\:\Rightarrow \\ $$$$\mathrm{S}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{8}}\mathrm{H}_{\mathrm{n}} −\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{H}_{\mathrm{n}+\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{H}_{\mathrm{n}+\mathrm{4}} −\frac{\mathrm{25}}{\mathrm{12}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{H}_{\mathrm{n}} +\mathrm{H}_{\mathrm{n}+\mathrm{4}} \right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{H}_{\mathrm{n}+\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{8}}−\frac{\mathrm{25}}{\mathrm{96}} \\ $$$$\mathrm{S}_{\mathrm{n}} \sim\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{logn}\:+\gamma\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}}\right)+\mathrm{log}\left(\mathrm{n}+\mathrm{4}\right)+\gamma\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{4}}\right)\right) \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{log}\left(\mathrm{n}+\mathrm{2}\right)+\gamma\:+\mathrm{o}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right)\right)\:+\frac{\mathrm{3}}{\mathrm{8}}−\frac{\mathrm{25}}{\mathrm{96}} \\ $$$$\mathrm{S}_{\mathrm{n}} \sim\mathrm{log}\left(\frac{\left(\mathrm{n}^{\mathrm{2}} \:+\mathrm{4n}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }{\left(\mathrm{n}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }\right)\:\:+\frac{\mathrm{3}}{\mathrm{8}}−\frac{\mathrm{25}}{\mathrm{96}}\:\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \frac{\left(\mathrm{n}^{\mathrm{2}} +\mathrm{4n}\right)^{\frac{\mathrm{1}}{\mathrm{8}}} }{\left(\mathrm{n}+\mathrm{2}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }=\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\smile\infty} \mathrm{S}_{\mathrm{n}} =\frac{\mathrm{3}}{\mathrm{8}}−\frac{\mathrm{25}}{\mathrm{96}}=\frac{\mathrm{36}−\mathrm{25}}{\mathrm{96}}=\frac{\mathrm{11}}{\mathrm{96}} \\ $$
Commented by mnjuly1970 last updated on 12/Jul/21
thx mr max...
$$\:\:\:{thx}\:{mr}\:{max}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *