Menu Close

S-n-k-1-n-k-2-1-k-C-n-k-please-help-

Tinku Tara 0 Comments
Pin




Question Number 108476 by pticantor last updated on 17/Aug/20
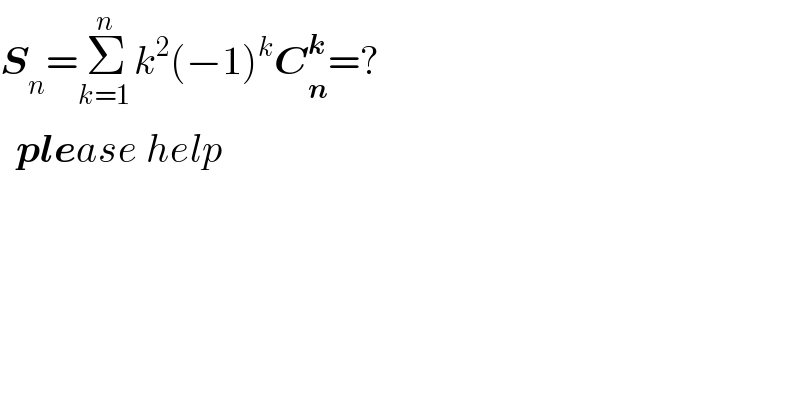
S_n =Σ_(k=1 ) ^n k^2 (−1)^k C_n ^k =? please help
$$\boldsymbol{{S}}_{{n}} =\underset{{k}=\mathrm{1}\:} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} \boldsymbol{{C}}_{\boldsymbol{{n}}} ^{\boldsymbol{{k}}} =? \\ $$$$\:\:\boldsymbol{{ple}}{ase}\:{help} \\ $$
Answered by mr W last updated on 17/Aug/20
(1−x)^n =Σ_(k=0) ^n (−1)^k C_n ^k x^k −n(1−x)^(n−1) =Σ_(k=0) ^n k(−1)^k C_n ^k x^(k−1) −n(1−x)^(n−1) x=Σ_(k=0) ^n k(−1)^k C_n ^k x^k n(n−1)(1−x)^(n−2) x−n(1−x)^(n−1) =Σ_(k=0) ^n k^2 (−1)^k C_n ^k x^(k−1) x=1: 0=Σ_(k=1) ^n k^2 (−1)^k C_n ^k
$$\left(\mathrm{1}−{x}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} {x}^{{k}} \\ $$$$−{n}\left(\mathrm{1}−{x}\right)^{{n}−\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} {x}^{{k}−\mathrm{1}} \\ $$$$−{n}\left(\mathrm{1}−{x}\right)^{{n}−\mathrm{1}} {x}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}\left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} {x}^{{k}} \\ $$$${n}\left({n}−\mathrm{1}\right)\left(\mathrm{1}−{x}\right)^{{n}−\mathrm{2}} {x}−{n}\left(\mathrm{1}−{x}\right)^{{n}−\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} {x}^{{k}−\mathrm{1}} \\ $$$${x}=\mathrm{1}: \\ $$$$\mathrm{0}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{k}} {C}_{{n}} ^{{k}} \\ $$
Answered by mathmax by abdo last updated on 17/Aug/20
let f(x) =Σ_(k=1) ^n (−1)^k C_n ^k x^k ⇒f(x) =Σ_(k=1) ^n C_n ^k (−x)^k =(1−x)^n ⇒Σ_(k=1) ^n k(−1)^k C_n ^k x^(k−1) =−n(1−x)^(n−1) ⇒ Σ_(k=1) ^n k(−1)^k C_n ^k x^k =−nx(1−x)^(n−1) ⇒ Σ_(k=1) ^n k^2 (−1)^k C_n ^k x^(k−1) =−n(1−x)^(n−1) ×n(n−1)x(1−x)^(n−2) x=1 ⇒Σ_(k=1) ^n k^2 (−1)^k C_n ^k =0
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \left(−\mathrm{x}\right)^{\mathrm{k}} \:=\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}} \\ $$$$\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}−\mathrm{1}} \:\:=−\mathrm{n}\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}} \:=−\mathrm{nx}\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:\mathrm{x}^{\mathrm{k}−\mathrm{1}} \:=−\mathrm{n}\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} ×\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{2}} \\ $$$$\mathrm{x}=\mathrm{1}\:\Rightarrow\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{k}^{\mathrm{2}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{n}} ^{\mathrm{k}} \:=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *