Menu Close

S-n-n-1-n-1-2-k-tanh-1-2-k-

Tinku Tara 0 Comments
Pin




Question Number 144272 by SOMEDAVONG last updated on 24/Jun/21
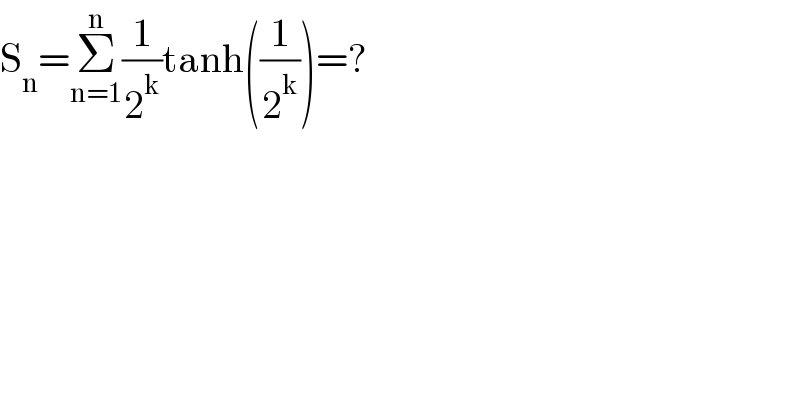
S_n =Σ_(n=1) ^n (1/2^k )tanh((1/2^k ))=?
$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{n}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\mathrm{tanh}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{k}} }\right)=? \\ $$
Answered by Olaf_Thorendsen last updated on 24/Jun/21
S_n = Σ_(k=1) ^n (1/2^k )tanh((x/2^k )) f_n (x) = Π_(k=1) ^n cosh((x/2^k )) (1) sinh2u = 2coshu.sinhhu coshu = ((sinh2u)/(2sinhu)) f_n (x) = Π_(k=1) ^n ((sinh((x/2^(k−1) )))/(2sinh((x/2^k )))) f_n (x) = (1/2^n ).((sinh(x))/(sinh((x/2^n )))) (2) (1) : lnf_n (x) = lnΠ_(k=1) ^n cosh((x/2^k )) lnf_n (x) = Σ_(k=1) ^n ln(cosh((x/2^k ))) (d/dx)lnf_n (x) = Σ_(k=1) ^n (1/2^k )tanh((x/2^k )) (d/dx)lnf_n (1) = Σ_(k=1) ^n (1/2^k )tanh((1/2^k )) = S_n (3) (2) : lnf_n (x) = ln(sinhx)−ln(sinh((x/2^n )))−nln2 (d/dx) lnf_n (x) = cothx−(1/2^n )coth((x/2^n )) (d/dx) lnf_n (1) = coth(1)−(1/2^n )coth((1/2^n )) (4) (3) and (4) : S_n = coth(1)−(1/2^n )coth((1/2^n )) S_n = ((e+e^(−1) )/(e−e^(−1) ))−(1/2^n ).((e^(1/2^n ) +e^(−(1/2^n )) )/(e^(1/2^n ) −e^(−(1/2^n )) )) S_n = ((e^2 +1)/(e^2 −1))−(1/2^n ).((e^(1/2^(n−1) ) +1)/(e^(1/2^(n−1) ) −1))
$$\mathrm{S}_{{n}} \:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\mathrm{tanh}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right) \\ $$$${f}_{{n}} \left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{cosh}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{sinh2}{u}\:=\:\mathrm{2cosh}{u}.\mathrm{sinhh}{u} \\ $$$$\mathrm{cosh}{u}\:=\:\frac{\mathrm{sinh2}{u}}{\mathrm{2sinh}{u}} \\ $$$${f}_{{n}} \left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\frac{\mathrm{sinh}\left(\frac{{x}}{\mathrm{2}^{{k}−\mathrm{1}} }\right)}{\mathrm{2sinh}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)} \\ $$$${f}_{{n}} \left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }.\frac{\mathrm{sinh}\left({x}\right)}{\mathrm{sinh}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)}\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{ln}{f}_{{n}} \left({x}\right)\:=\:\mathrm{ln}\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{cosh}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right) \\ $$$$\mathrm{ln}{f}_{{n}} \left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{ln}\left(\mathrm{cosh}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right)\right) \\ $$$$\frac{{d}}{{dx}}\mathrm{ln}{f}_{{n}} \left({x}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\mathrm{tanh}\left(\frac{{x}}{\mathrm{2}^{{k}} }\right) \\ $$$$\frac{{d}}{{dx}}\mathrm{ln}{f}_{{n}} \left(\mathrm{1}\right)\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\mathrm{tanh}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\:=\:\mathrm{S}_{{n}} \:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\::\:\mathrm{ln}{f}_{{n}} \left({x}\right)\:=\:\mathrm{ln}\left(\mathrm{sinh}{x}\right)−\mathrm{ln}\left(\mathrm{sinh}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\right)−{n}\mathrm{ln2} \\ $$$$\frac{{d}}{{dx}}\:\mathrm{ln}{f}_{{n}} \left({x}\right)\:=\:\mathrm{coth}{x}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\mathrm{coth}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right) \\ $$$$\frac{{d}}{{dx}}\:\mathrm{ln}{f}_{{n}} \left(\mathrm{1}\right)\:=\:\mathrm{coth}\left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\mathrm{coth}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\:\:\:\:\:\left(\mathrm{4}\right) \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\:\mathrm{and}\:\left(\mathrm{4}\right)\:: \\ $$$$\mathrm{S}_{{n}} \:=\:\mathrm{coth}\left(\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\mathrm{coth}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right) \\ $$$$\mathrm{S}_{{n}} \:=\:\frac{{e}+{e}^{−\mathrm{1}} }{{e}−{e}^{−\mathrm{1}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }.\frac{{e}^{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }} +{e}^{−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }} }{{e}^{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }} −{e}^{−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }} } \\ $$$$\mathrm{S}_{{n}} \:=\:\frac{{e}^{\mathrm{2}} +\mathrm{1}}{{e}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }.\frac{{e}^{\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }} +\mathrm{1}}{{e}^{\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }} −\mathrm{1}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *