Menu Close

S-x-2-1-x-1-x-3-1-x-2-x-n-1-x-n-1-t-1-x-n-t-Can-you-evaluate-S-

Tinku Tara 0 Comments
Pin




Question Number 13097 by FilupS last updated on 14/May/17
S=Σ_(x_2 =1) ^x_1 Σ_(x_3 =1) ^x_2 ∙∙∙Σ_(x_n =1) ^x_(n−1) Σ_(t=1) ^x_n t Can you evaluate S?
S=∑x1x2=1∑x2x3=1⋅⋅⋅∑xn−1xn=1∑xnt=1tCanyouevaluateS?
Answered by nume1114 last updated on 15/May/17
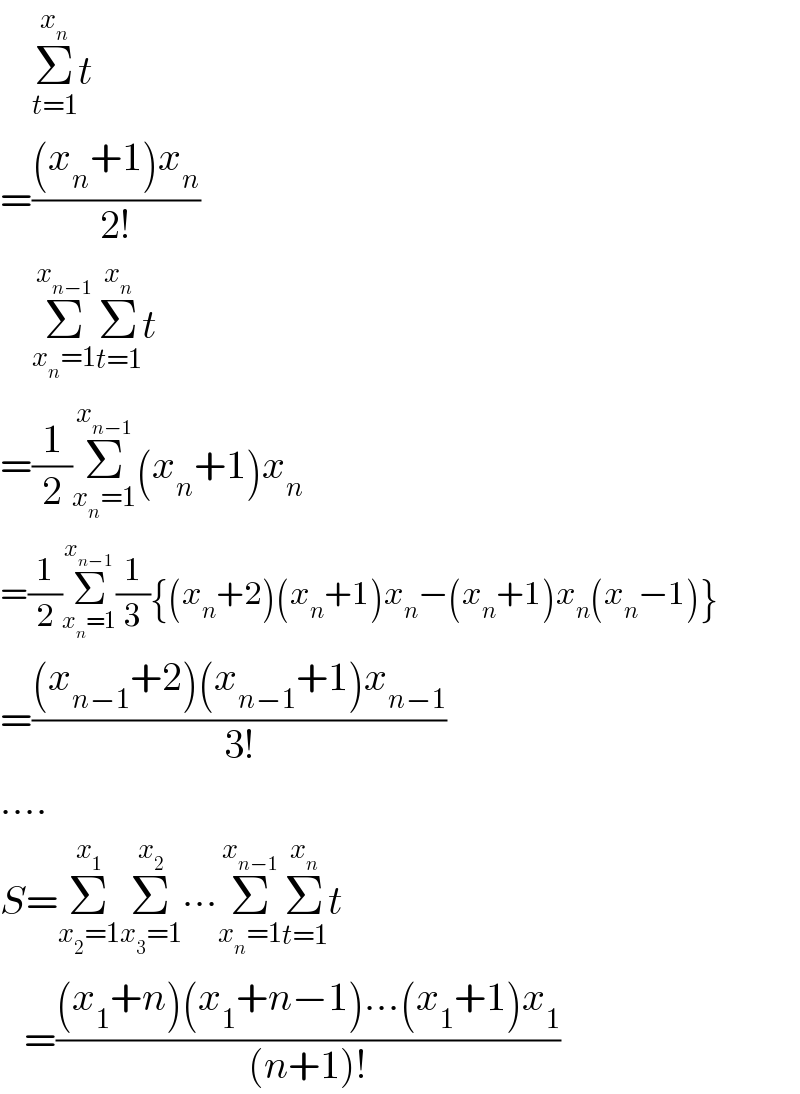
Σ_(t=1) ^x_n t =(((x_n +1)x_n )/(2!)) Σ_(x_n =1) ^x_(n−1) Σ_(t=1) ^x_n t =(1/2)Σ_(x_n =1) ^x_(n−1) (x_n +1)x_n =(1/2)Σ_(x_n =1) ^x_(n−1) (1/3){(x_n +2)(x_n +1)x_n −(x_n +1)x_n (x_n −1)} =(((x_(n−1) +2)(x_(n−1) +1)x_(n−1) )/(3!)) .... S=Σ_(x_2 =1) ^x_1 Σ_(x_3 =1) ^x_2 ∙∙∙Σ_(x_n =1) ^x_(n−1) Σ_(t=1) ^x_n t =(((x_1 +n)(x_1 +n−1)...(x_1 +1)x_1 )/((n+1)!))
∑xnt=1t=(xn+1)xn2!∑xn−1xn=1∑xnt=1t=12∑xn−1xn=1(xn+1)xn=12∑xn−1xn=113{(xn+2)(xn+1)xn−(xn+1)xn(xn−1)}=(xn−1+2)(xn−1+1)xn−13!….S=∑x1x2=1∑x2x3=1⋅⋅⋅∑xn−1xn=1∑xnt=1t=(x1+n)(x1+n−1)…(x1+1)x1(n+1)!
Commented by mrW1 last updated on 16/May/17
Nice!
Nice!

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *