Question Number 182347 by SANOGO last updated on 08/Dec/22
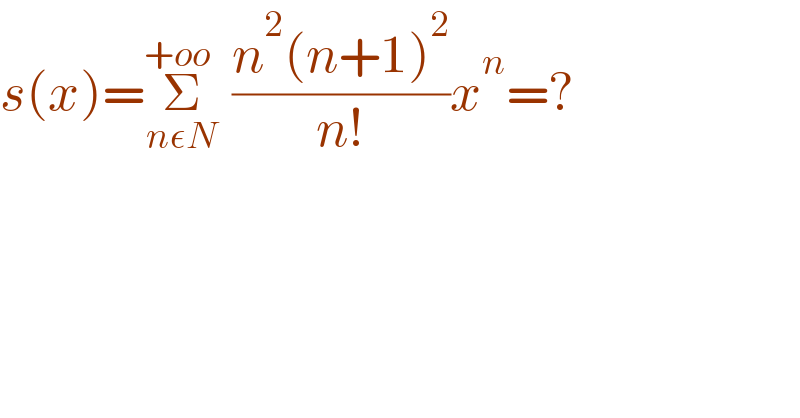
$${s}\left({x}\right)=\underset{{n}\epsilon{N}} {\overset{+{oo}\:\:} {\sum}}\:\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }{{n}!}{x}^{{n}} =? \\ $$
Answered by mr W last updated on 08/Dec/22

$${e}^{{x}} −\mathrm{1}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!} \\ $$$${e}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{nx}^{{n}−\mathrm{1}} }{{n}!} \\ $$$${xe}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{nx}^{{n}} }{{n}!} \\ $$$$\left({x}+\mathrm{1}\right){e}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} }{{n}!} \\ $$$$\left({x}^{\mathrm{3}} +{x}^{\mathrm{2}} \right){e}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} {x}^{{n}+\mathrm{1}} }{{n}!} \\ $$$$\left({x}^{\mathrm{3}} +\mathrm{4}{x}^{\mathrm{2}} +\mathrm{2}{x}\right){e}^{\mathrm{3}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right){x}^{{n}} }{{n}!} \\ $$$$\left({x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} \right){e}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} }{{n}!} \\ $$$$\left({x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{3}} +\mathrm{14}{x}^{\mathrm{2}} +\mathrm{4}{x}\right){e}^{{x}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} {x}^{{n}} }{{n}!} \\ $$$$\Rightarrow{S}\left({x}\right)=\left({x}^{\mathrm{4}} +\mathrm{8}{x}^{\mathrm{3}} +\mathrm{14}{x}^{\mathrm{2}} +\mathrm{4}{x}\right){e}^{{x}} \\ $$
Commented by SEKRET last updated on 08/Dec/22

$$\:\:\boldsymbol{\mathrm{super}}\: \\ $$
