Question Number 180082 by a.lgnaoui last updated on 07/Nov/22
![Sachant que A_1 A_2 =10cm: ∡AAB=75^° 1−Determiner l ′angle x 2−Determiner la distance A_1 A6 3−Determiner la hauteur[h]=A_6 B](https://www.tinkutara.com/question/Q180082.png)
$${Sachant}\:{que}\:\:\mathrm{A}_{\mathrm{1}} \mathrm{A}_{\mathrm{2}} =\mathrm{10}{cm}:\:\measuredangle\mathrm{AAB}=\mathrm{75}^{°} \\ $$$$\mathrm{1}−{Determiner}\:{l}\:'{angle}\:{x} \\ $$$$\mathrm{2}−{Determiner}\:{la}\:{distance}\:\mathrm{A}_{\mathrm{1}} \mathrm{A6} \\ $$$$\mathrm{3}−{Determiner}\:{la}\:{hauteur}\left[{h}\right]=\mathrm{A}_{\mathrm{6}} \mathrm{B} \\ $$
Commented by a.lgnaoui last updated on 07/Nov/22

Commented by CElcedricjunior last updated on 07/Nov/22

$$\left.\mathrm{1}\right)\boldsymbol{{x}}=\mathrm{15}^{\mathrm{0}} \\ $$$$\left.\mathrm{2}\right)\boldsymbol{{A}}_{\mathrm{1}} \boldsymbol{{A}}_{\mathrm{6}} ={A}_{\mathrm{1}} {A}_{\mathrm{2}} +{A}_{\mathrm{2}} {A}_{\mathrm{4}} +\boldsymbol{{A}}_{\mathrm{4}} \boldsymbol{{A}}_{\mathrm{6}} \\ $$$$=\mathrm{10}+^{\mathrm{10}} \frac{\boldsymbol{{sin}}\mathrm{120}}{\boldsymbol{{sin}}\mathrm{30}}+\:\mathrm{10}\frac{\boldsymbol{{sin}}\mathrm{60}}{\boldsymbol{{sin}}\mathrm{60}} \\ $$$$=\mathrm{10}+\mathrm{10}×\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}+\mathrm{10} \\ $$$$=\mathrm{20}+\mathrm{10}\sqrt{\mathrm{3}}=\mathrm{10}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$${A}_{\mathrm{1}} \boldsymbol{{A}}_{\mathrm{6}} =\mathrm{10}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\left.\mathrm{3}\right)\boldsymbol{{tan}}\mathrm{15}^{\mathrm{0}} =\frac{\boldsymbol{{h}}}{\boldsymbol{{A}}_{\mathrm{1}} \boldsymbol{{A}}_{\mathrm{6}} } \\ $$$$=>\boldsymbol{{h}}=\boldsymbol{{A}}_{\mathrm{1}} \boldsymbol{{A}}_{\mathrm{6}} \boldsymbol{{tan}}\mathrm{15}^{\mathrm{0}} \\ $$$$=>\boldsymbol{{h}}=\mathrm{10}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}} \\ $$$$=>\boldsymbol{{h}}=\mathrm{10}\sqrt{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}=\mathrm{10} \\ $$
Commented by a.lgnaoui last updated on 07/Nov/22

$${thanks}\:{for}\:{you} \\ $$
Answered by mr W last updated on 07/Nov/22

Commented by CElcedricjunior last updated on 07/Nov/22
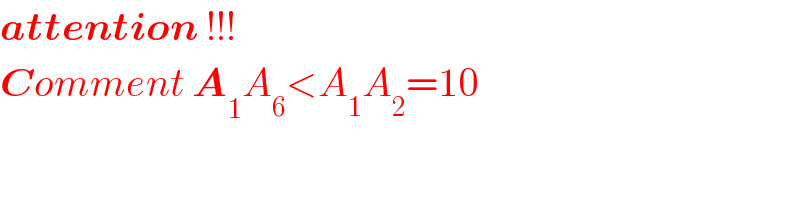
$$\boldsymbol{{attention}}\:!!! \\ $$$$\boldsymbol{{C}}{omment}\:\boldsymbol{{A}}_{\mathrm{1}} {A}_{\mathrm{6}} <{A}_{\mathrm{1}} {A}_{\mathrm{2}} =\mathrm{10} \\ $$
Commented by mr W last updated on 07/Nov/22

$$\mathrm{75}={x}+\mathrm{4}{x}=\mathrm{5}{x} \\ $$$$\Rightarrow{x}=\mathrm{15}° \\ $$$$ \\ $$$${say}\:{A}_{\mathrm{1}} {A}_{\mathrm{2}} ={A}_{\mathrm{2}} {A}_{\mathrm{3}} =…={A}_{\mathrm{5}} {A}_{\mathrm{6}} =\mathrm{1} \\ $$$$\frac{{A}_{\mathrm{1}} {A}_{\mathrm{6}} }{\mathrm{sin}\:\mathrm{75}}=\frac{{A}_{\mathrm{5}} {A}_{\mathrm{6}} }{\mathrm{sin}\:\mathrm{15}} \\ $$$${A}_{\mathrm{1}} {A}_{\mathrm{6}} =\frac{\mathrm{sin}\:\mathrm{75}}{\mathrm{sin}\:\mathrm{15}}=\frac{\mathrm{1}}{\mathrm{tan}\:\mathrm{15}}=\frac{\mathrm{1}}{\:\mathrm{2}−\sqrt{\mathrm{3}}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$ \\ $$$${h}={A}_{\mathrm{1}} {A}_{\mathrm{6}} ×\mathrm{tan}\:\mathrm{15}=\mathrm{1} \\ $$$${or} \\ $$$$\angle{A}_{\mathrm{1}} {BA}_{\mathrm{6}} =\mathrm{90}−\mathrm{15}=\mathrm{75}° \\ $$$$\Rightarrow{h}={A}_{\mathrm{5}} {A}_{\mathrm{6}} =\mathrm{1} \\ $$
Commented by mr W last updated on 07/Nov/22

$${you}\:{should}\:{have}\:{seen}\:{that}\:{i}\:{assumed} \\ $$$${A}_{\mathrm{1}} {A}_{\mathrm{2}} =\mathrm{1}.\:{that}\:{means}\:{i}\:{used}\:{the}\:{unit} \\ $$$${dm},\:{not}\:{cm}. \\ $$
Commented by a.lgnaoui last updated on 07/Nov/22

$${thanks}\:{for}\:{you}\:{too}. \\ $$$${h}=\mathrm{1}{dm}=\mathrm{10}{cm} \\ $$
