Question Number 91689 by john santu last updated on 02/May/20
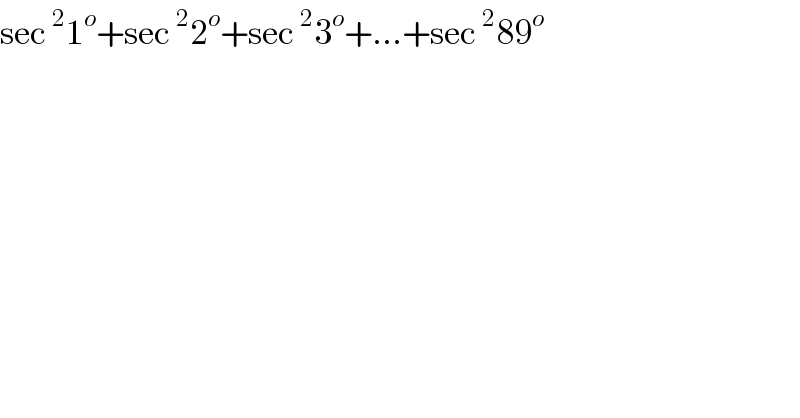
$$\mathrm{sec}\:^{\mathrm{2}} \mathrm{1}^{{o}} +\mathrm{sec}\:^{\mathrm{2}} \mathrm{2}^{{o}} +\mathrm{sec}\:^{\mathrm{2}} \mathrm{3}^{{o}} +…+\mathrm{sec}\:^{\mathrm{2}} \mathrm{89}^{{o}} \\ $$
Commented by Prithwish Sen 1 last updated on 02/May/20
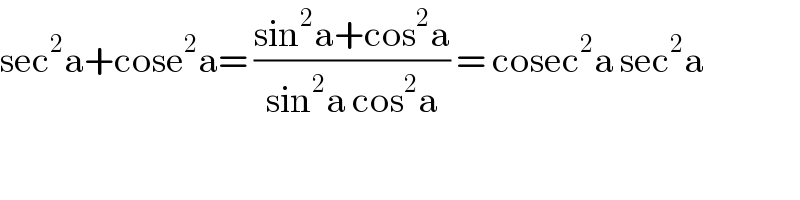
$$\mathrm{sec}^{\mathrm{2}} \mathrm{a}+\mathrm{cose}^{\mathrm{2}} \mathrm{a}=\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{a}+\mathrm{cos}^{\mathrm{2}} \mathrm{a}}{\mathrm{sin}^{\mathrm{2}} \mathrm{a}\:\mathrm{cos}^{\mathrm{2}} \mathrm{a}}\:=\:\mathrm{cosec}^{\mathrm{2}} \mathrm{a}\:\mathrm{sec}^{\mathrm{2}} \mathrm{a} \\ $$
Commented by Prithwish Sen 1 last updated on 02/May/20
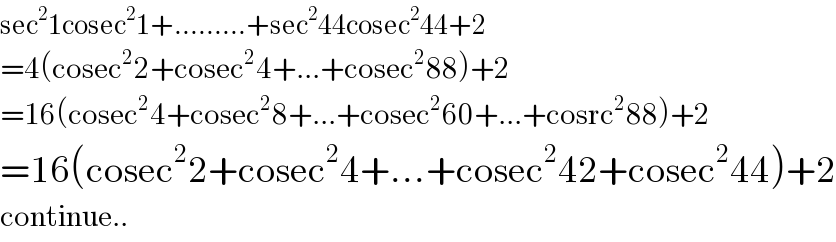
$$\mathrm{sec}^{\mathrm{2}} \mathrm{1cosec}^{\mathrm{2}} \mathrm{1}+………+\mathrm{sec}^{\mathrm{2}} \mathrm{44cosec}^{\mathrm{2}} \mathrm{44}+\mathrm{2} \\ $$$$=\mathrm{4}\left(\mathrm{cosec}^{\mathrm{2}} \mathrm{2}+\mathrm{cosec}^{\mathrm{2}} \mathrm{4}+…+\mathrm{cosec}^{\mathrm{2}} \mathrm{88}\right)+\mathrm{2} \\ $$$$=\mathrm{16}\left(\mathrm{cosec}^{\mathrm{2}} \mathrm{4}+\mathrm{cosec}^{\mathrm{2}} \mathrm{8}+…+\mathrm{cosec}^{\mathrm{2}} \mathrm{60}+…+\mathrm{cosrc}^{\mathrm{2}} \mathrm{88}\right)+\mathrm{2} \\ $$$$=\mathrm{16}\left(\mathrm{cosec}^{\mathrm{2}} \mathrm{2}+\mathrm{cosec}^{\mathrm{2}} \mathrm{4}+…+\mathrm{cosec}^{\mathrm{2}} \mathrm{42}+\mathrm{cosec}^{\mathrm{2}} \mathrm{44}\right)+\mathrm{2} \\ $$$$\mathrm{continue}.. \\ $$
Commented by jagoll last updated on 02/May/20
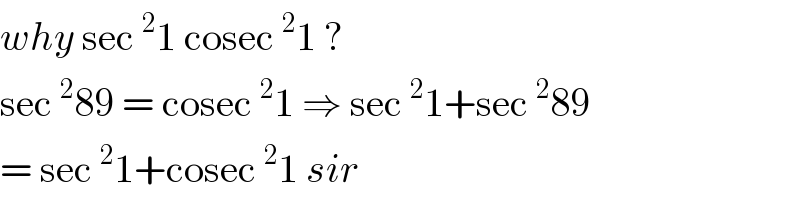
$${why}\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{1}\:\mathrm{cosec}\:^{\mathrm{2}} \mathrm{1}\:? \\ $$$$\mathrm{sec}\:^{\mathrm{2}} \mathrm{89}\:=\:\mathrm{cosec}\:^{\mathrm{2}} \mathrm{1}\:\Rightarrow\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{1}+\mathrm{sec}\:^{\mathrm{2}} \mathrm{89} \\ $$$$=\:\mathrm{sec}\:^{\mathrm{2}} \mathrm{1}+\mathrm{cosec}\:^{\mathrm{2}} \mathrm{1}\:{sir} \\ $$
Commented by jagoll last updated on 02/May/20
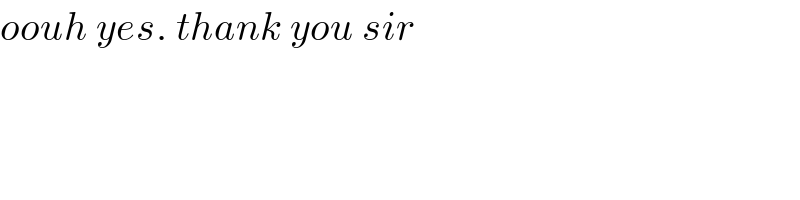
$${oouh}\:{yes}.\:{thank}\:{you}\:{sir} \\ $$
Commented by jagoll last updated on 02/May/20
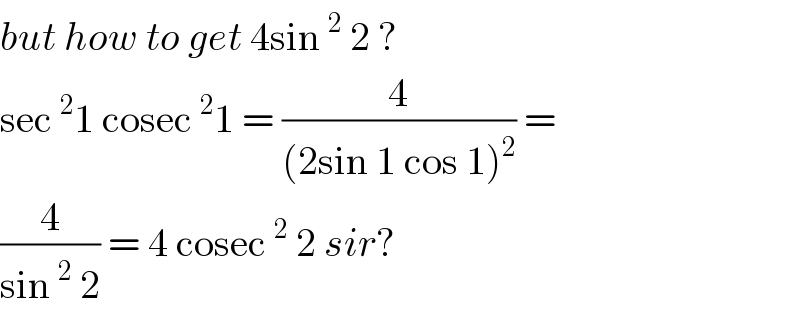
$${but}\:{how}\:{to}\:{get}\:\mathrm{4sin}\:^{\mathrm{2}} \:\mathrm{2}\:? \\ $$$$\mathrm{sec}\:^{\mathrm{2}} \mathrm{1}\:\mathrm{cosec}\:^{\mathrm{2}} \mathrm{1}\:=\:\frac{\mathrm{4}}{\left(\mathrm{2sin}\:\mathrm{1}\:\mathrm{cos}\:\mathrm{1}\right)^{\mathrm{2}} }\:= \\ $$$$\frac{\mathrm{4}}{\mathrm{sin}\:^{\mathrm{2}} \:\mathrm{2}}\:=\:\mathrm{4}\:\mathrm{cosec}\:^{\mathrm{2}} \:\mathrm{2}\:{sir}? \\ $$
