Menu Close

sec-2-tan-2-9-tan-2-d-

Tinku Tara 0 Comments
Pin




Question Number 117496 by bemath last updated on 12/Oct/20
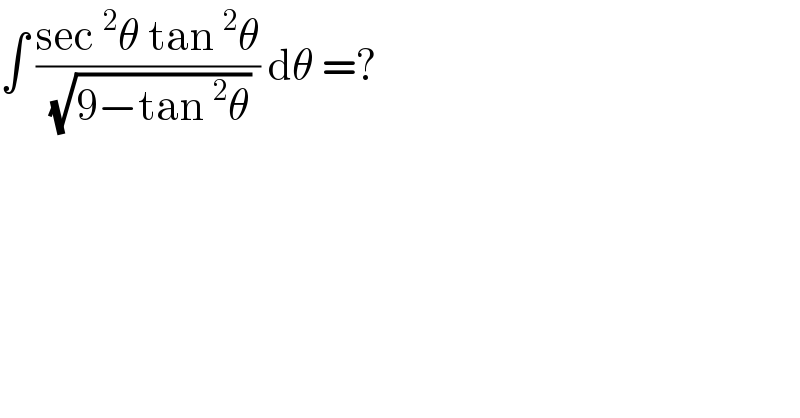
∫ ((sec^2 θ tan^2 θ)/( (√(9−tan^2 θ)))) dθ =?
$$\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \theta\:\mathrm{tan}\:^{\mathrm{2}} \theta}{\:\sqrt{\mathrm{9}−\mathrm{tan}\:^{\mathrm{2}} \theta}}\:\mathrm{d}\theta\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 12/Oct/20
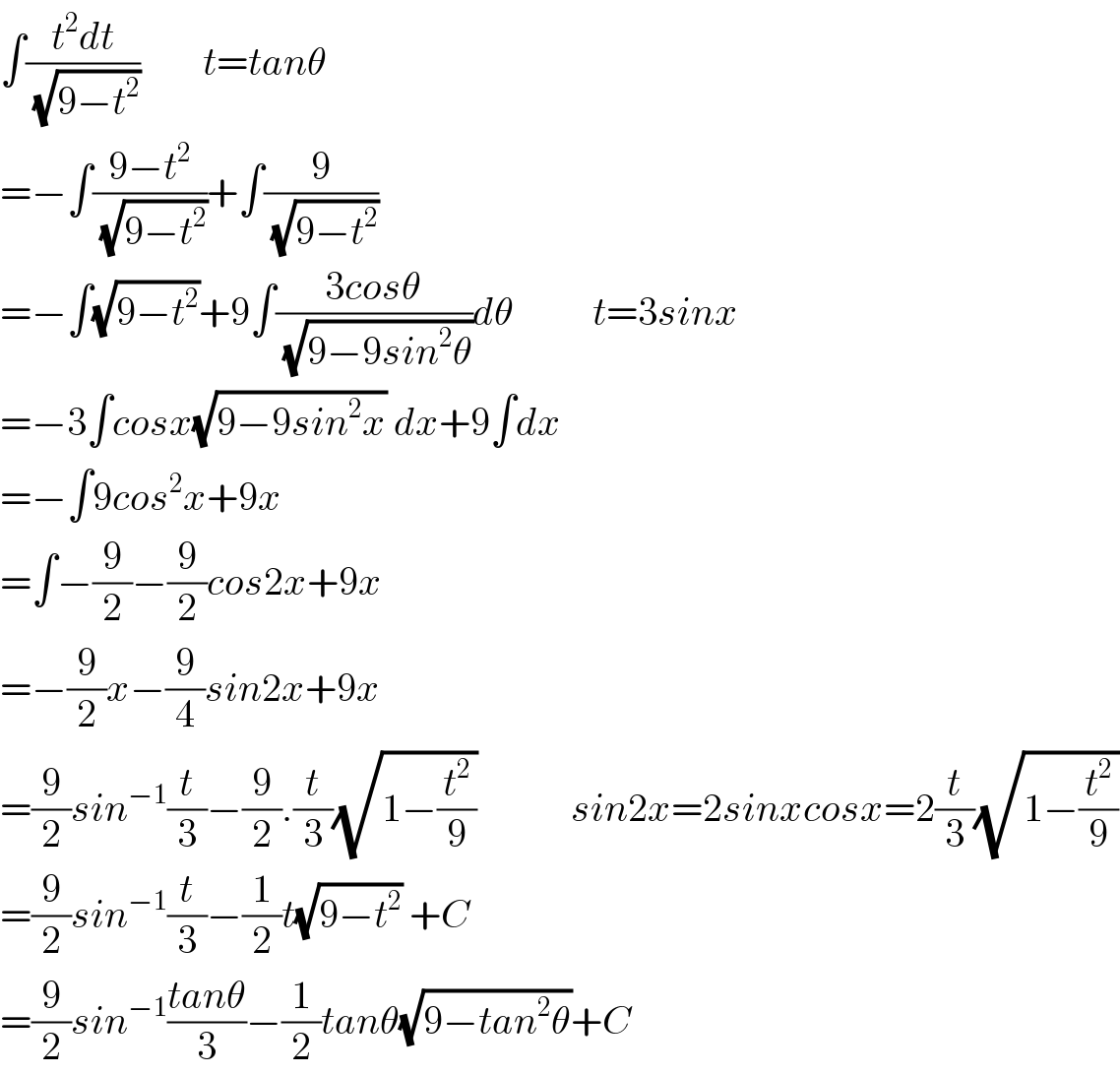
∫((t^2 dt)/( (√(9−t^2 )))) t=tanθ =−∫((9−t^2 )/( (√(9−t^2 ))))+∫(9/( (√(9−t^2 )))) =−∫(√(9−t^2 ))+9∫((3cosθ)/( (√(9−9sin^2 θ))))dθ t=3sinx =−3∫cosx(√(9−9sin^2 x)) dx+9∫dx =−∫9cos^2 x+9x =∫−(9/2)−(9/2)cos2x+9x =−(9/2)x−(9/4)sin2x+9x =(9/2)sin^(−1) (t/3)−(9/2).(t/3)(√(1−(t^2 /9))) sin2x=2sinxcosx=2(t/3)(√(1−(t^2 /9))) =(9/2)sin^(−1) (t/3)−(1/2)t(√(9−t^2 )) +C =(9/2)sin^(−1) ((tanθ)/3)−(1/2)tanθ(√(9−tan^2 θ))+C
$$\int\frac{{t}^{\mathrm{2}} {dt}}{\:\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }}\:\:\:\:\:\:\:\:{t}={tan}\theta \\ $$$$=−\int\frac{\mathrm{9}−{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }}+\int\frac{\mathrm{9}}{\:\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }} \\ $$$$=−\int\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }+\mathrm{9}\int\frac{\mathrm{3}{cos}\theta}{\:\sqrt{\mathrm{9}−\mathrm{9}{sin}^{\mathrm{2}} \theta}}{d}\theta\:\:\:\:\:\:\:\:\:\:{t}=\mathrm{3}{sinx} \\ $$$$=−\mathrm{3}\int{cosx}\sqrt{\mathrm{9}−\mathrm{9}{sin}^{\mathrm{2}} {x}}\:{dx}+\mathrm{9}\int{dx}\:\:\: \\ $$$$=−\int\mathrm{9}{cos}^{\mathrm{2}} {x}+\mathrm{9}{x} \\ $$$$=\int−\frac{\mathrm{9}}{\mathrm{2}}−\frac{\mathrm{9}}{\mathrm{2}}{cos}\mathrm{2}{x}+\mathrm{9}{x} \\ $$$$=−\frac{\mathrm{9}}{\mathrm{2}}{x}−\frac{\mathrm{9}}{\mathrm{4}}{sin}\mathrm{2}{x}+\mathrm{9}{x} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{t}}{\mathrm{3}}−\frac{\mathrm{9}}{\mathrm{2}}.\frac{{t}}{\mathrm{3}}\sqrt{\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{9}}}\:\:\:\:\:\:\:\:\:\:\:\:{sin}\mathrm{2}{x}=\mathrm{2}{sinxcosx}=\mathrm{2}\frac{{t}}{\mathrm{3}}\sqrt{\mathrm{1}−\frac{{t}^{\mathrm{2}} }{\mathrm{9}}} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{t}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}{t}\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }\:+{C} \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}{sin}^{−\mathrm{1}} \frac{{tan}\theta}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}{tan}\theta\sqrt{\mathrm{9}−{tan}^{\mathrm{2}} \theta}+{C} \\ $$
Answered by MJS_new last updated on 12/Oct/20
∫((sec^2 θ tan^2 θ)/( (√(9−tan^2 θ))))dθ= [t=tan θ → dθ=(dt/(t^2 +1))] =∫(t^2 /( (√(9−t^2 ))))dt= [u=arcsin (t/3) → dt=(√(9−t^2 ))du] =9∫sin^2 u du=(9/2)∫1−cos 2u du= =(9/2)u−(9/4)sin 2u =(9/2)u−(9/2)sin u cos u = =(9/2)arcsin (t/3) −((t(√(9−t^2 )))/2)= =(9/2)arcsin ((tan x)/3) −((tan x (√(9−tan^2 x)))/2)+C
$$\int\frac{\mathrm{sec}^{\mathrm{2}} \:\theta\:\mathrm{tan}^{\mathrm{2}} \:\theta}{\:\sqrt{\mathrm{9}−\mathrm{tan}^{\mathrm{2}} \:\theta}}{d}\theta= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\theta\:\rightarrow\:{d}\theta=\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\int\frac{{t}^{\mathrm{2}} }{\:\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\mathrm{arcsin}\:\frac{{t}}{\mathrm{3}}\:\rightarrow\:{dt}=\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }{du}\right] \\ $$$$=\mathrm{9}\int\mathrm{sin}^{\mathrm{2}} \:{u}\:{du}=\frac{\mathrm{9}}{\mathrm{2}}\int\mathrm{1}−\mathrm{cos}\:\mathrm{2}{u}\:{du}= \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}{u}−\frac{\mathrm{9}}{\mathrm{4}}\mathrm{sin}\:\mathrm{2}{u}\:=\frac{\mathrm{9}}{\mathrm{2}}{u}−\frac{\mathrm{9}}{\mathrm{2}}\mathrm{sin}\:{u}\:\mathrm{cos}\:{u}\:= \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\mathrm{arcsin}\:\frac{{t}}{\mathrm{3}}\:−\frac{{t}\sqrt{\mathrm{9}−{t}^{\mathrm{2}} }}{\mathrm{2}}= \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\mathrm{arcsin}\:\frac{\mathrm{tan}\:{x}}{\mathrm{3}}\:−\frac{\mathrm{tan}\:{x}\:\sqrt{\mathrm{9}−\mathrm{tan}^{\mathrm{2}} \:{x}}}{\mathrm{2}}+{C} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *