sec-2-x-e-tanx-dx-

Question Number 33644 by mondodotto@gmail.com last updated on 21/Apr/18

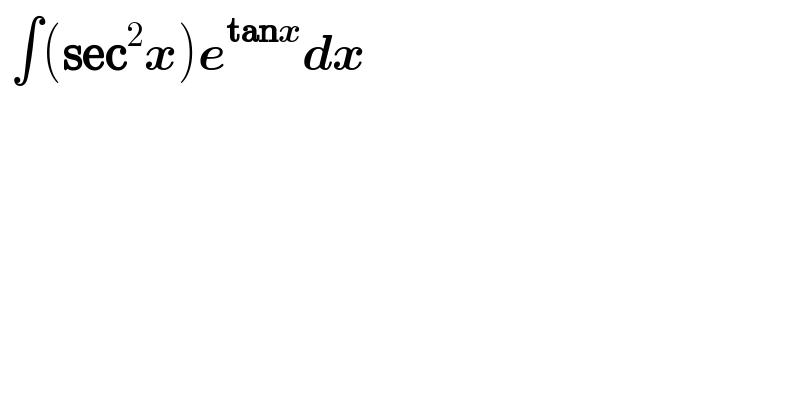
\int (\sec^{2} x) e^{\tan x} d x

Answered by Joel578 last updated on 21/Apr/18

I = \int (\sec^{2} x) e^{\tan x} d x

u = \tan x \to d u = \sec^{2} x d x

I = \int e^{u} d u

= e^{u} + C = e^{\tan x} + C

Facebook Tweet Pin