Question Number 97239 by john santu last updated on 07/Jun/20
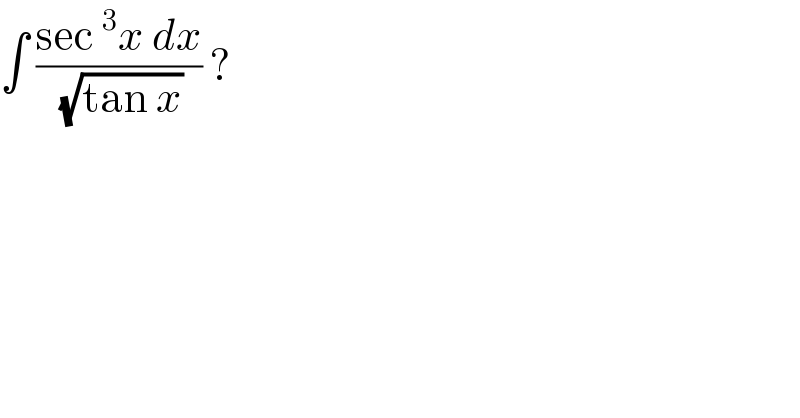
$$\int\:\frac{\mathrm{sec}\:^{\mathrm{3}} {x}\:{dx}}{\:\sqrt{\mathrm{tan}\:{x}}}\:?\: \\ $$
Commented by MJS last updated on 07/Jun/20
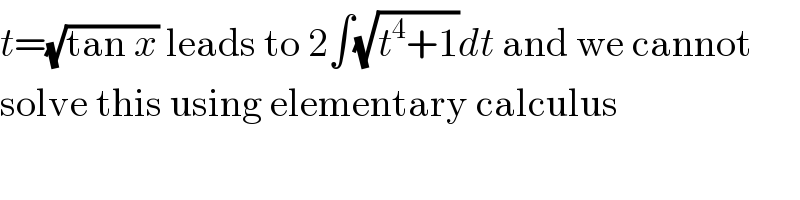
$${t}=\sqrt{\mathrm{tan}\:{x}}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{2}\int\sqrt{{t}^{\mathrm{4}} +\mathrm{1}}{dt}\:\mathrm{and}\:\mathrm{we}\:\mathrm{cannot} \\ $$$$\mathrm{solve}\:\mathrm{this}\:\mathrm{using}\:\mathrm{elementary}\:\mathrm{calculus} \\ $$
Commented by john santu last updated on 07/Jun/20
yes, i can't solve that integral
Commented by MJS last updated on 07/Jun/20
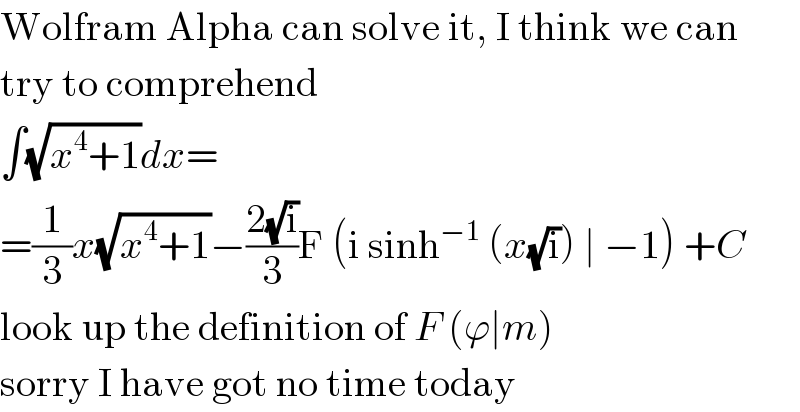
$$\mathrm{Wolfram}\:\mathrm{Alpha}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it},\:\mathrm{I}\:\mathrm{think}\:\mathrm{we}\:\mathrm{can} \\ $$$$\mathrm{try}\:\mathrm{to}\:\mathrm{comprehend} \\ $$$$\int\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{x}\sqrt{{x}^{\mathrm{4}} +\mathrm{1}}−\frac{\mathrm{2}\sqrt{\mathrm{i}}}{\mathrm{3}}\mathrm{F}\:\left(\mathrm{i}\:\mathrm{sinh}^{−\mathrm{1}} \:\left({x}\sqrt{\mathrm{i}}\right)\:\mid\:−\mathrm{1}\right)\:+{C} \\ $$$$\mathrm{look}\:\mathrm{up}\:\mathrm{the}\:\mathrm{definition}\:\mathrm{of}\:{F}\:\left(\varphi\mid{m}\right) \\ $$$$\mathrm{sorry}\:\mathrm{I}\:\mathrm{have}\:\mathrm{got}\:\mathrm{no}\:\mathrm{time}\:\mathrm{today} \\ $$
