Question Number 14181 by tawa tawa last updated on 29/May/17
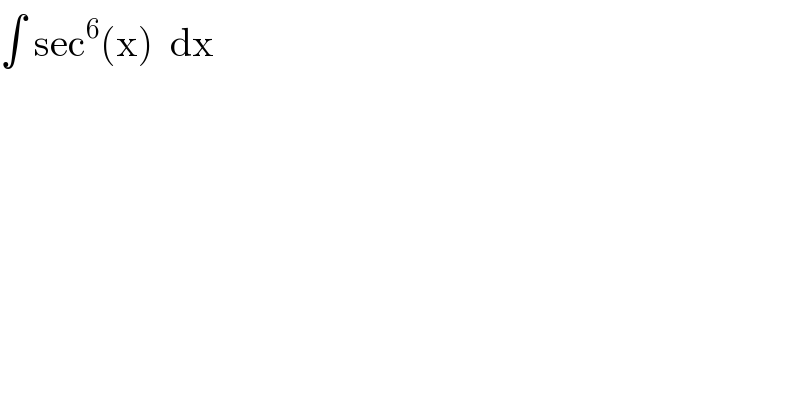
$$\int\:\mathrm{sec}^{\mathrm{6}} \left(\mathrm{x}\right)\:\:\mathrm{dx}\:\: \\ $$
Answered by ajfour last updated on 29/May/17
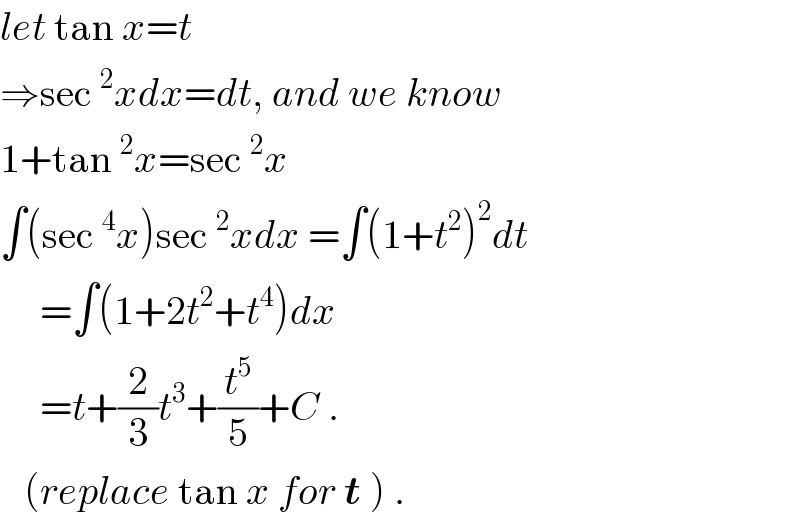
$${let}\:\mathrm{tan}\:{x}={t} \\ $$$$\Rightarrow\mathrm{sec}\:^{\mathrm{2}} {xdx}={dt},\:{and}\:{we}\:{know} \\ $$$$\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} {x}=\mathrm{sec}\:^{\mathrm{2}} {x} \\ $$$$\int\left(\mathrm{sec}\:^{\mathrm{4}} {x}\right)\mathrm{sec}\:^{\mathrm{2}} {xdx}\:=\int\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} {dt} \\ $$$$\:\:\:\:\:=\int\left(\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \right){dx} \\ $$$$\:\:\:\:\:={t}+\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} +\frac{{t}^{\mathrm{5}} }{\mathrm{5}}+{C}\:. \\ $$$$\:\:\:\left({replace}\:\mathrm{tan}\:{x}\:{for}\:\boldsymbol{{t}}\:\right)\:. \\ $$
Commented by tawa tawa last updated on 29/May/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
