Menu Close

sec-d-

Tinku Tara 0 Comments
Pin




Question Number 96613 by s.ayeni14@yahoo.com last updated on 03/Jun/20
∫secθdθ
$$\int\mathrm{sec}\theta\mathrm{d}\theta \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
∫sec(θ)((sec(θ)+tan(θ))/(sec(θ)+tan(θ)))dθ =ln∣sec(θ)+tan(θ)∣+c i have more than 9 ways to solve this integral i will post them later
$$\int{sec}\left(\theta\right)\frac{{sec}\left(\theta\right)+{tan}\left(\theta\right)}{{sec}\left(\theta\right)+{tan}\left(\theta\right)}{d}\theta \\ $$$$={ln}\mid{sec}\left(\theta\right)+{tan}\left(\theta\right)\mid+{c} \\ $$$${i}\:{have}\:{more}\:{than}\:\mathrm{9}\:{ways}\:{to}\:{solve}\:{this} \\ $$$${integral}\:{i}\:{will}\:{post}\:{them}\:{later} \\ $$
Commented by s.ayeni14@yahoo.com last updated on 03/Jun/20
ok sir
$$\mathrm{ok}\:\mathrm{sir} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
=∫sec(x)+tan(x)−tan(x) dx =∫((1−sin(x))/(cos(x)))dx+∫tan(x)dx =∫((cos(x))/(1+sin(x)))dx+∫((sin(x))/(cos(x)))dx ln∣1+sin(x)∣−ln∣cos(x)∣+c
$$=\int{sec}\left({x}\right)+{tan}\left({x}\right)−{tan}\left({x}\right)\:{dx} \\ $$$$=\int\frac{\mathrm{1}−{sin}\left({x}\right)}{{cos}\left({x}\right)}{dx}+\int{tan}\left({x}\right){dx} \\ $$$$=\int\frac{{cos}\left({x}\right)}{\mathrm{1}+{sin}\left({x}\right)}{dx}+\int\frac{{sin}\left({x}\right)}{{cos}\left({x}\right)}{dx} \\ $$$${ln}\mid\mathrm{1}+{sin}\left({x}\right)\mid−{ln}\mid{cos}\left({x}\right)\mid+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
=∫(1/(sin((π/2)−x)))dx =∫(1/(2sin((π/4)−x)cos((π/4)−x))).((sec^2 ((π/4)−(x/2)))/(sec^2 ((π/4)−(x/2))))dx =(1/2)∫((sec^2 ((π/4)−(x/2)))/(tan((π/4)−(x/2))))dx =−ln∣tan((π/4)−(x/2))∣+c
$$=\int\frac{\mathrm{1}}{{sin}\left(\frac{\pi}{\mathrm{2}}−{x}\right)}{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{4}}−{x}\right){cos}\left(\frac{\pi}{\mathrm{4}}−{x}\right)}.\frac{{sec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{{sec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sec}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{{tan}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$=−{ln}\mid{tan}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\mid+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
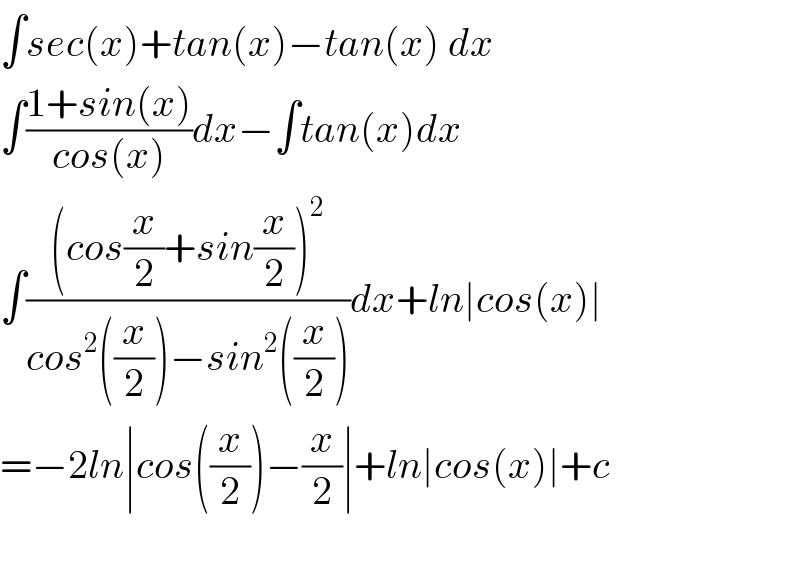
∫sec(x)+tan(x)−tan(x) dx ∫((1+sin(x))/(cos(x)))dx−∫tan(x)dx ∫(((cos(x/2)+sin(x/2))^2 )/(cos^2 ((x/2))−sin^2 ((x/2))))dx+ln∣cos(x)∣ =−2ln∣cos((x/2))−(x/2)∣+ln∣cos(x)∣+c
$$\int{sec}\left({x}\right)+{tan}\left({x}\right)−{tan}\left({x}\right)\:{dx} \\ $$$$\int\frac{\mathrm{1}+{sin}\left({x}\right)}{{cos}\left({x}\right)}{dx}−\int{tan}\left({x}\right){dx} \\ $$$$\int\frac{\left({cos}\frac{{x}}{\mathrm{2}}+{sin}\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx}+{ln}\mid{cos}\left({x}\right)\mid \\ $$$$=−\mathrm{2}{ln}\mid{cos}\left(\frac{{x}}{\mathrm{2}}\right)−\frac{{x}}{\mathrm{2}}\mid+{ln}\mid{cos}\left({x}\right)\mid+{c} \\ $$$$ \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
=∫sec(x)((tan(x))/(tan(x)))dx =∫((sec(x)tan(x))/( (√(sec^2 (x)−1))))dx =cosh^(−1) (sec(x))+c
$$=\int{sec}\left({x}\right)\frac{{tan}\left({x}\right)}{{tan}\left({x}\right)}{dx} \\ $$$$=\int\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\:\sqrt{{sec}^{\mathrm{2}} \left({x}\right)−\mathrm{1}}}{dx} \\ $$$$={cosh}^{−\mathrm{1}} \left({sec}\left({x}\right)\right)+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
∫((sin(x))/(sin(x)cos(x)))dx ∫((sin(x))/(cos(x)(√(1−cos^2 (x)))))dx =sech^(−1) (cos(x))+c
$$\int\frac{{sin}\left({x}\right)}{{sin}\left({x}\right){cos}\left({x}\right)}{dx} \\ $$$$\int\frac{{sin}\left({x}\right)}{{cos}\left({x}\right)\sqrt{\mathrm{1}−{cos}^{\mathrm{2}} \left({x}\right)}}{dx} \\ $$$$={sech}^{−\mathrm{1}} \left({cos}\left({x}\right)\right)+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
∫((csc(x))/(cot(x)))dx ∫((csc(x)cot(x))/(cot(x)))dx ∫((−1)/(csc^2 (x)−1))d(csc(x)) coth^(−1) (csc(x))+c
$$\int\frac{{csc}\left({x}\right)}{{cot}\left({x}\right)}{dx} \\ $$$$\int\frac{{csc}\left({x}\right){cot}\left({x}\right)}{{cot}\left({x}\right)}{dx} \\ $$$$\int\frac{−\mathrm{1}}{{csc}^{\mathrm{2}} \left({x}\right)−\mathrm{1}}{d}\left({csc}\left({x}\right)\right) \\ $$$${coth}^{−\mathrm{1}} \left({csc}\left({x}\right)\right)+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
∫(1/(cos^2 ((x/2))−sin^2 ((x/2)))).((sec^2 ((x/2)))/(sec^2 ((x/2))))dx ∫((sec^2 ((x/2)))/(1−tan^2 ((x/2))))dx 2∫((−(1/2)sec^2 ((x/2)))/(tan^2 ((x/2))−1))dx =2coth^(−1) (tan((x/2)))+c
$$\int\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−{sin}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}.\frac{{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$\int\frac{{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$\mathrm{2}\int\frac{−\frac{\mathrm{1}}{\mathrm{2}}{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{1}}{dx} \\ $$$$=\mathrm{2}{coth}^{−\mathrm{1}} \left({tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
∫((csc(x))/(cot(x)))dx ∫((csc^2 (x))/(csc(x)cot(x)))dx ∫((csc^2 (x))/(cot(x)(√(cot^2 (x)+1))))dx csch^(−1) (cot(x))+c
$$\int\frac{{csc}\left({x}\right)}{{cot}\left({x}\right)}{dx} \\ $$$$\int\frac{{csc}^{\mathrm{2}} \left({x}\right)}{{csc}\left({x}\right){cot}\left({x}\right)}{dx} \\ $$$$\int\frac{{csc}^{\mathrm{2}} \left({x}\right)}{{cot}\left({x}\right)\sqrt{{cot}^{\mathrm{2}} \left({x}\right)+\mathrm{1}}}{dx} \\ $$$${csch}^{−\mathrm{1}} \left({cot}\left({x}\right)\right)+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
∫((sec^2 ((x/2)))/(1−tan^2 ((x/2))))dx ∫((tan((x/2))sec^2 ((x/2)))/(((√(1−tan^2 ((x/2)))))^2 tan(x/2)))dx ∫(1/( (√(1−tan^2 ((x/2))))(√(1−((√(1−tan^2 (x/2))))^2 )))).((2tan(x/2) sec^2 (x/2))/(2(√(1−tan^2 (x/2)))))dx =2sech^(−1) (√(1−tan^2 ((x/2))))+c
$$\int\frac{{sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$\int\frac{{tan}\left(\frac{{x}}{\mathrm{2}}\right){sec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\left(\sqrt{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\right)^{\mathrm{2}} {tan}\frac{{x}}{\mathrm{2}}}{dx} \\ $$$$\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\sqrt{\mathrm{1}−\left(\sqrt{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}\right)^{\mathrm{2}} }}.\frac{\mathrm{2}{tan}\frac{{x}}{\mathrm{2}}\:{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{1}−{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}}{dx} \\ $$$$=\mathrm{2}{sech}^{−\mathrm{1}} \sqrt{\mathrm{1}−{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
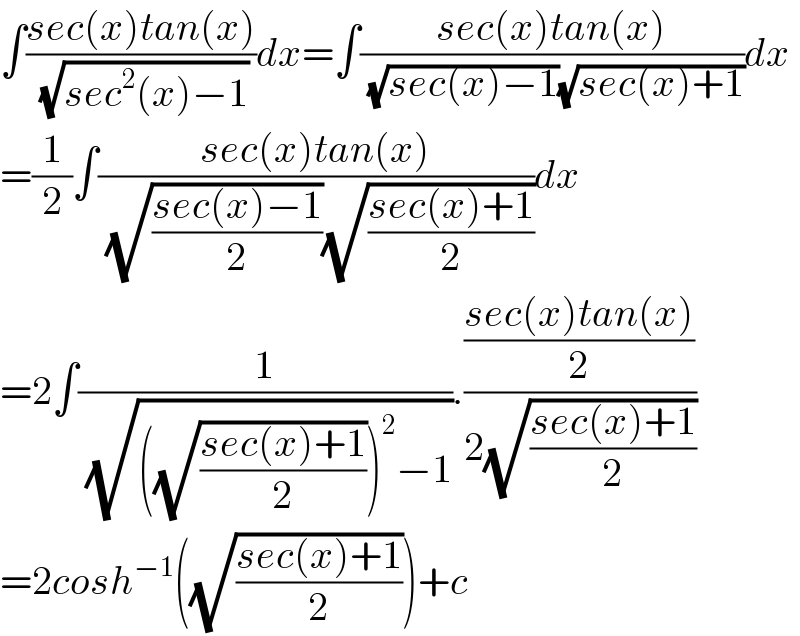
∫((sec(x)tan(x))/( (√(sec^2 (x)−1))))dx=∫((sec(x)tan(x))/( (√(sec(x)−1))(√(sec(x)+1))))dx =(1/2)∫((sec(x)tan(x))/( (√((sec(x)−1)/2))(√((sec(x)+1)/2))))dx =2∫(1/( (√(((√((sec(x)+1)/2)))^2 −1)))).(((sec(x)tan(x))/2)/(2(√((sec(x)+1)/2)))) =2cosh^(−1) ((√((sec(x)+1)/2)))+c
$$\int\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\:\sqrt{{sec}^{\mathrm{2}} \left({x}\right)−\mathrm{1}}}{dx}=\int\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\:\sqrt{{sec}\left({x}\right)−\mathrm{1}}\sqrt{{sec}\left({x}\right)+\mathrm{1}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\:\sqrt{\frac{{sec}\left({x}\right)−\mathrm{1}}{\mathrm{2}}}\sqrt{\frac{{sec}\left({x}\right)+\mathrm{1}}{\mathrm{2}}}}{dx} \\ $$$$=\mathrm{2}\int\frac{\mathrm{1}}{\:\sqrt{\left(\sqrt{\frac{{sec}\left({x}\right)+\mathrm{1}}{\mathrm{2}}}\right)^{\mathrm{2}} −\mathrm{1}}}.\frac{\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\mathrm{2}}}{\mathrm{2}\sqrt{\frac{{sec}\left({x}\right)+\mathrm{1}}{\mathrm{2}}}} \\ $$$$=\mathrm{2}{cosh}^{−\mathrm{1}} \left(\sqrt{\frac{{sec}\left({x}\right)+\mathrm{1}}{\mathrm{2}}}\right)+{c} \\ $$
Answered by  M±th+et+s last updated on 03/Jun/20
∫sec(x)dx=∫((sec(x)tan(x))/( (√(sec^2 (x)−1))))dx =(1/2)∫((sec(x)tan(x))/( (√((sec(x)−1)/2))(√((sec(x)+1)/2))))dx =∫(1/( (√(((sec(x)−1)/2)+1)))).((sec(x)tan(x))/(2(√((sec(x)−1)/2))))dx =2sinh^− ((√((sec(x)−1)/2)))+c and mybe there are another ways
$$\int{sec}\left({x}\right){dx}=\int\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\:\sqrt{{sec}^{\mathrm{2}} \left({x}\right)−\mathrm{1}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\:\sqrt{\frac{{sec}\left({x}\right)−\mathrm{1}}{\mathrm{2}}}\sqrt{\frac{{sec}\left({x}\right)+\mathrm{1}}{\mathrm{2}}}}{dx} \\ $$$$=\int\frac{\mathrm{1}}{\:\sqrt{\frac{{sec}\left({x}\right)−\mathrm{1}}{\mathrm{2}}+\mathrm{1}}}.\frac{{sec}\left({x}\right){tan}\left({x}\right)}{\mathrm{2}\sqrt{\frac{{sec}\left({x}\right)−\mathrm{1}}{\mathrm{2}}}}{dx} \\ $$$$=\mathrm{2}{sinh}^{−} \left(\sqrt{\frac{{sec}\left({x}\right)−\mathrm{1}}{\mathrm{2}}}\right)+{c} \\ $$$$ \\ $$$${and}\:{mybe}\:{there}\:{are}\:{another}\:{ways} \\ $$
Answered by Rio Michael last updated on 03/Jun/20
hahahaha great work sir! but one method left. ∫ sec θ dθ = ∫((sec θ( sec θ + tan θ))/(sec θ + tan θ)) dθ = ∫((sec^2 θ + secθ tanθ)/(sec θ + tan θ)) dθ let u = sec θ + tan θ ⇒ du = (sec θ tanθ + sec^2 θ)dθ = (sec^2 θ + secθ tanθ)dθ ⇒ ∫ sec θ dθ = ∫(du/u) after substitution = ln∣u∣ + k ⇒ ∫sec θ dθ = ln∣ sec θ +tan θ∣ + k
$$\mathrm{hahahaha}\:\mathrm{great}\:\mathrm{work}\:\mathrm{sir}! \\ $$$$\mathrm{but}\:\mathrm{one}\:\mathrm{method}\:\mathrm{left}. \\ $$$$\:\int\:\mathrm{sec}\:\theta\:{d}\theta\:=\:\int\frac{\mathrm{sec}\:\theta\left(\:\mathrm{sec}\:\theta\:+\:\mathrm{tan}\:\theta\right)}{\mathrm{sec}\:\theta\:+\:\mathrm{tan}\:\theta}\:{d}\theta\:=\:\int\frac{\mathrm{sec}^{\mathrm{2}} \theta\:+\:\mathrm{sec}\theta\:\mathrm{tan}\theta}{\mathrm{sec}\:\theta\:+\:\mathrm{tan}\:\theta}\:{d}\theta \\ $$$$\mathrm{let}\:{u}\:=\:\mathrm{sec}\:\theta\:+\:\mathrm{tan}\:\theta\:\Rightarrow\:{du}\:=\:\left(\mathrm{sec}\:\theta\:\mathrm{tan}\theta\:+\:\mathrm{sec}^{\mathrm{2}} \theta\right){d}\theta\:\:=\:\left(\mathrm{sec}^{\mathrm{2}} \theta\:+\:\mathrm{sec}\theta\:\mathrm{tan}\theta\right){d}\theta \\ $$$$\:\Rightarrow\:\int\:\mathrm{sec}\:\theta\:{d}\theta\:=\:\int\frac{{du}}{{u}}\:\mathrm{after}\:\mathrm{substitution}\:=\:\mathrm{ln}\mid{u}\mid\:+\:{k} \\ $$$$\Rightarrow\:\int\mathrm{sec}\:\theta\:{d}\theta\:=\:\mathrm{ln}\mid\:\mathrm{sec}\:\theta\:+\mathrm{tan}\:\theta\mid\:+\:{k} \\ $$$$\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *