sec-x-dx-

Question Number 101272 by bemath last updated on 01/Jul/20

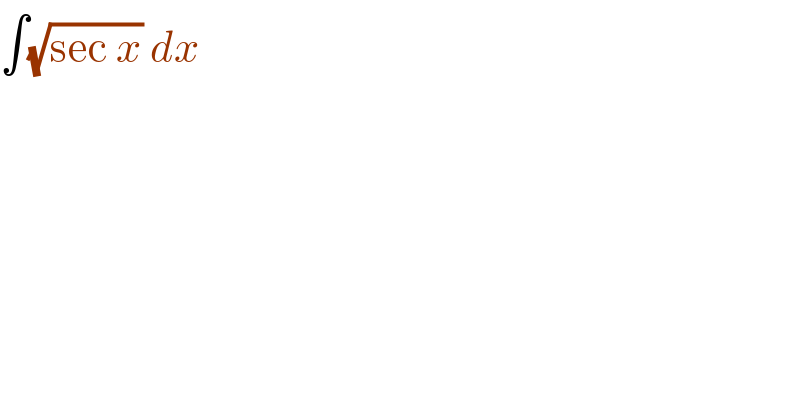
$$\int\sqrt{\mathrm{sec}\:{x}}\:{dx}\: \\ $$

Commented by john santu last updated on 01/Jul/20

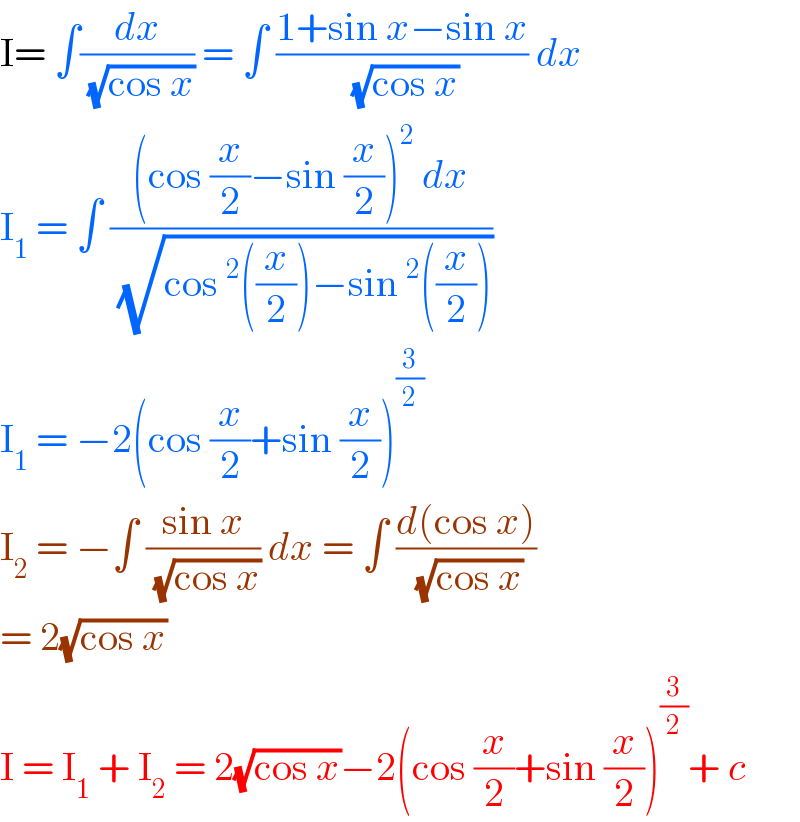
I= ∫(dx/( (√(cos x)))) = ∫ ((1+sin x−sin x)/( (√(cos x)))) dx I_1 = ∫ (((cos (x/2)−sin (x/2))^2 dx)/( (√(cos^2 ((x/2))−sin^2 ((x/2)))))) I_1 = −2(cos (x/2)+sin (x/2))^(3/2) I_2 = −∫ ((sin x)/( (√(cos x)))) dx = ∫ ((d(cos x))/( (√(cos x)))) = 2(√(cos x)) I = I_1 + I_2 = 2(√(cos x))−2(cos (x/2)+sin (x/2))^(3/2) + c

$$\mathrm{I}=\:\int\frac{{dx}}{\:\sqrt{\mathrm{cos}\:{x}}}\:=\:\int\:\frac{\mathrm{1}+\mathrm{sin}\:{x}−\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{cos}\:{x}}}\:{dx} \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:\int\:\frac{\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} \:{dx}}{\:\sqrt{\mathrm{cos}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−\mathrm{sin}\:^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}} \\ $$$$\mathrm{I}_{\mathrm{1}} \:=\:−\mathrm{2}\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \\ $$$$\mathrm{I}_{\mathrm{2}} \:=\:−\int\:\frac{\mathrm{sin}\:{x}}{\:\sqrt{\mathrm{cos}\:{x}}}\:{dx}\:=\:\int\:\frac{{d}\left(\mathrm{cos}\:{x}\right)}{\:\sqrt{\mathrm{cos}\:{x}}} \\ $$$$=\:\mathrm{2}\sqrt{\mathrm{cos}\:{x}} \\ $$$$\mathrm{I}\:=\:\mathrm{I}_{\mathrm{1}} \:+\:\mathrm{I}_{\mathrm{2}} \:=\:\mathrm{2}\sqrt{\mathrm{cos}\:{x}}−\mathrm{2}\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\:{c}\: \\ $$

Commented by MJS last updated on 01/Jul/20

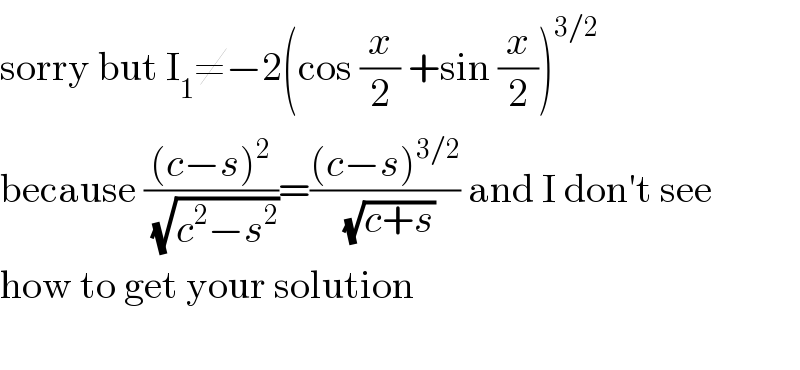
sorry but I_1 ≠−2(cos (x/2) +sin (x/2))^(3/2) because (((c−s)^2 )/( (√(c^2 −s^2 ))))=(((c−s)^(3/2) )/( (√(c+s)))) and I don′t see how to get your solution

$$\mathrm{sorry}\:\mathrm{but}\:\mathrm{I}_{\mathrm{1}} \neq−\mathrm{2}\left(\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\:+\mathrm{sin}\:\frac{{x}}{\mathrm{2}}\right)^{\mathrm{3}/\mathrm{2}} \\ $$$$\mathrm{because}\:\frac{\left({c}−{s}\right)^{\mathrm{2}} }{\:\sqrt{{c}^{\mathrm{2}} −{s}^{\mathrm{2}} }}=\frac{\left({c}−{s}\right)^{\mathrm{3}/\mathrm{2}} }{\:\sqrt{{c}+{s}}}\:\mathrm{and}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{see} \\ $$$$\mathrm{how}\:\mathrm{to}\:\mathrm{get}\:\mathrm{your}\:\mathrm{solution} \\ $$$$ \\ $$

Answered by mathmax by abdo last updated on 01/Jul/20

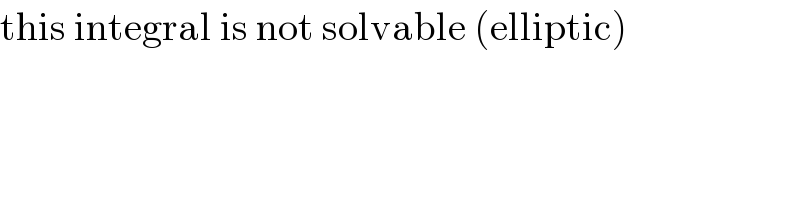
this integral is not solvable (elliptic)

$$\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{not}\:\mathrm{solvable}\:\left(\mathrm{elliptic}\right) \\ $$

Commented by MJS last updated on 01/Jul/20

$$\mathrm{yes}\:\mathrm{you}\:\mathrm{are}\:\mathrm{right} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply