Question Number 115498 by bobhans last updated on 26/Sep/20

$$\int\:\mathrm{sec}\:{x}\:{dx}\:? \\ $$$$\int\:\sqrt{{x}−\sqrt{{x}}}\:{dx}\:? \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left(\sqrt[{{n}\:}]{\mathrm{1}+\sqrt{\mathrm{1}+{n}^{\mathrm{2}} }}\right)\left(\sqrt[{{n}\:}]{\mathrm{2}+\sqrt{\mathrm{4}+{n}^{\mathrm{2}} }}\right)\left(\sqrt[{{n}\:}]{\mathrm{3}+\sqrt{\mathrm{9}+{n}^{\mathrm{2}} }}\right)…\left(\sqrt[{{n}\:}]{{n}+\sqrt{\mathrm{2}{n}^{\mathrm{2}} }}\right)}{{n}}? \\ $$
Commented by bobhans last updated on 26/Sep/20
$${thank}\:{you}\:{all}\:{master}…\: \\ $$
Commented by Dwaipayan Shikari last updated on 26/Sep/20
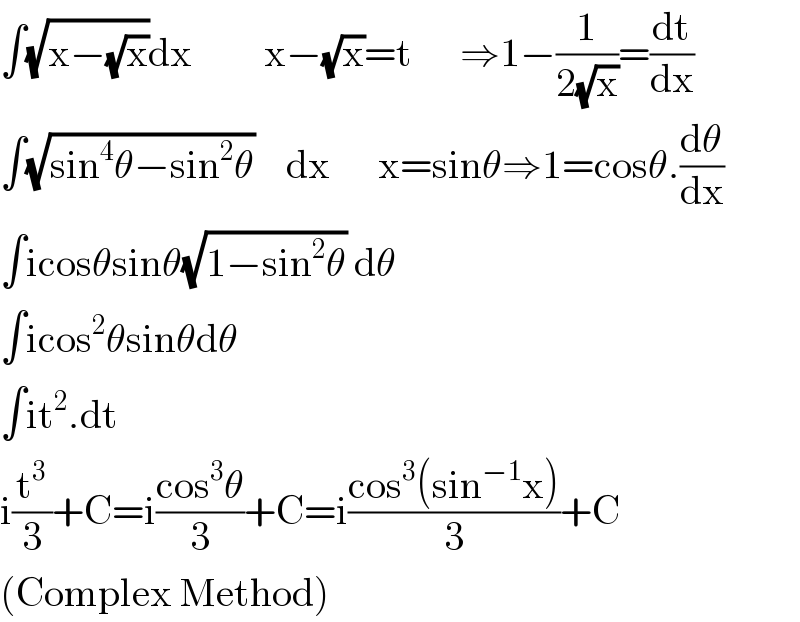
$$\int\sqrt{\mathrm{x}−\sqrt{\mathrm{x}}}\mathrm{dx}\:\:\:\:\:\:\:\:\:\mathrm{x}−\sqrt{\mathrm{x}}=\mathrm{t}\:\:\:\:\:\:\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}=\frac{\mathrm{dt}}{\mathrm{dx}} \\ $$$$\int\sqrt{\mathrm{sin}^{\mathrm{4}} \theta−\mathrm{sin}^{\mathrm{2}} \theta}\:\:\:\:\mathrm{dx}\:\:\:\:\:\:\mathrm{x}=\mathrm{sin}\theta\Rightarrow\mathrm{1}=\mathrm{cos}\theta.\frac{\mathrm{d}\theta}{\mathrm{dx}} \\ $$$$\int\mathrm{icos}\theta\mathrm{sin}\theta\sqrt{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta}\:\mathrm{d}\theta \\ $$$$\int\mathrm{icos}^{\mathrm{2}} \theta\mathrm{sin}\theta\mathrm{d}\theta \\ $$$$\int\mathrm{it}^{\mathrm{2}} .\mathrm{dt} \\ $$$$\mathrm{i}\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{C}=\mathrm{i}\frac{\mathrm{cos}^{\mathrm{3}} \theta}{\mathrm{3}}+\mathrm{C}=\mathrm{i}\frac{\mathrm{cos}^{\mathrm{3}} \left(\mathrm{sin}^{−\mathrm{1}} \mathrm{x}\right)}{\mathrm{3}}+\mathrm{C} \\ $$$$\left(\mathrm{Complex}\:\mathrm{Method}\right) \\ $$
Answered by bemath last updated on 26/Sep/20
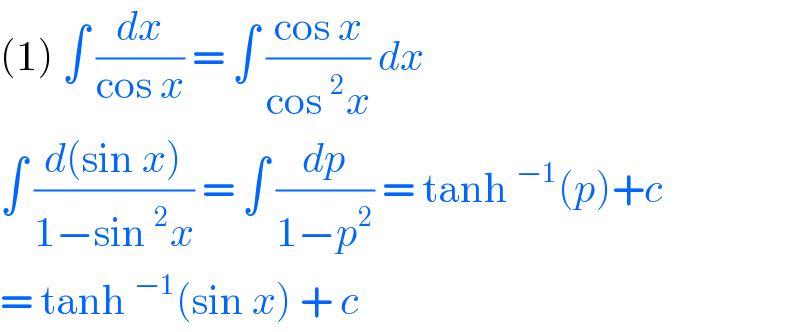
$$\left(\mathrm{1}\right)\:\int\:\frac{{dx}}{\mathrm{cos}\:{x}}\:=\:\int\:\frac{\mathrm{cos}\:{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\: \\ $$$$\int\:\frac{{d}\left(\mathrm{sin}\:{x}\right)}{\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} {x}}\:=\:\int\:\frac{{dp}}{\mathrm{1}−{p}^{\mathrm{2}} }\:=\:\mathrm{tanh}\:^{−\mathrm{1}} \left({p}\right)+{c} \\ $$$$=\:\mathrm{tanh}\:^{−\mathrm{1}} \left(\mathrm{sin}\:{x}\right)\:+\:{c}\: \\ $$
Answered by $@y@m last updated on 26/Sep/20
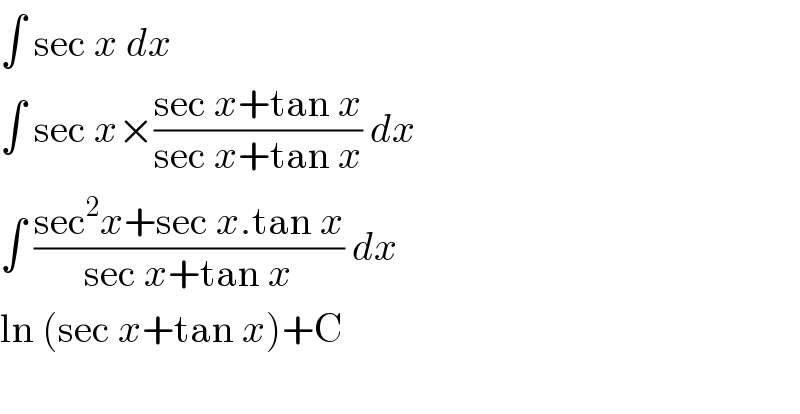
$$\int\:\mathrm{sec}\:{x}\:{dx}\: \\ $$$$\int\:\mathrm{sec}\:{x}×\frac{\mathrm{sec}\:{x}+\mathrm{tan}\:{x}}{\mathrm{sec}\:{x}+\mathrm{tan}\:{x}}\:{dx}\: \\ $$$$\int\:\frac{\mathrm{sec}^{\mathrm{2}} {x}+\mathrm{sec}\:{x}.\mathrm{tan}\:{x}}{\mathrm{sec}\:{x}+\mathrm{tan}\:{x}}\:{dx}\: \\ $$$$\mathrm{ln}\:\left(\mathrm{sec}\:{x}+\mathrm{tan}\:{x}\right)+\mathrm{C} \\ $$$$ \\ $$
Answered by TANMAY PANACEA last updated on 26/Sep/20
![lim_(n→∞) (((1+(√(1^2 +n^2 ))))^(1/n) /n^(1/n) )×(((2+(√(2^2 +n^2 ))))^(1/n) /n^(1/n) )×..(((n+(√(n^2 +n^2 ))))^(1/n) /n^(1/n) ) look general term (((r+(√(r^2 +n^2 )))/n))^(1/n) →((r/n)+(√(1+(r^2 /n^2 ))) )^(1/n) i have done error...so correcting now y=lim_(n→∞) Π((r/n)+(√(1+(r^2 /n^2 ))) )^(1/n) lny=lim_(n→∞) (1/n)[ln((1/n)+(√(1+(1^2 /n^2 ))) )+ln((2/n)+(√(1+(2^2 /n^2 ))) )+...ln((n/n)+(√(1+(n^2 /n^2 ))) )] lny=∫_0 ^1 ln(x+(√(1+x^2 )) )dx general term =(((r+(√(r^2 +))))^(1/n) /)](https://www.tinkutara.com/question/Q115504.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{li}{m}}\:\frac{\sqrt[{{n}}]{\mathrm{1}+\sqrt{\mathrm{1}^{\mathrm{2}} +{n}^{\mathrm{2}} }}}{{n}^{\frac{\mathrm{1}}{{n}}} }×\frac{\sqrt[{{n}}]{\mathrm{2}+\sqrt{\mathrm{2}^{\mathrm{2}} +{n}^{\mathrm{2}} }}}{{n}^{\frac{\mathrm{1}}{{n}}} }×..\frac{\sqrt[{{n}}]{{n}+\sqrt{{n}^{\mathrm{2}} +{n}^{\mathrm{2}} }}}{{n}^{\frac{\mathrm{1}}{{n}}} } \\ $$$${look}\:{general}\:{term} \\ $$$$\left(\frac{{r}+\sqrt{{r}^{\mathrm{2}} +{n}^{\mathrm{2}} }}{{n}}\right)^{\frac{\mathrm{1}}{{n}}} \rightarrow\left(\frac{{r}}{{n}}+\sqrt{\mathrm{1}+\frac{{r}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$${i}\:{have}\:{done}\:{error}…{so}\:{correcting}\:{now} \\ $$$${y}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\Pi\left(\frac{{r}}{{n}}+\sqrt{\mathrm{1}+\frac{{r}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$${lny}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}}\left[{ln}\left(\frac{\mathrm{1}}{{n}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\right)+{ln}\left(\frac{\mathrm{2}}{{n}}+\sqrt{\mathrm{1}+\frac{\mathrm{2}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\right)+…{ln}\left(\frac{{n}}{{n}}+\sqrt{\mathrm{1}+\frac{{n}^{\mathrm{2}} }{{n}^{\mathrm{2}} }}\:\right)\right] \\ $$$${lny}=\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right){dx} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${general}\:{term}\:=\frac{\sqrt[{{n}}]{{r}+\sqrt{{r}^{\mathrm{2}} +}}}{} \\ $$$$ \\ $$
Commented by bemath last updated on 26/Sep/20
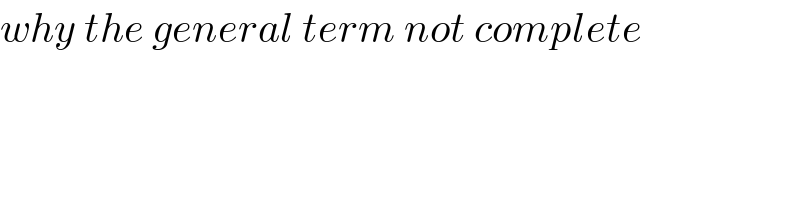
$${why}\:{the}\:{general}\:{term}\:{not}\:{complete} \\ $$
Answered by Dwaipayan Shikari last updated on 26/Sep/20
![Π_(r=1) ^n ((r/n)+(√((r^2 /n^2 )+1)))^(1/n) =y (1/n)Σ_(r=1) ^n log((r/n)+(√((r^2 /n^2 )+1)))=logy ∫_0 ^1 log(x+(√(x^2 +1)))dx [xlog(x+(√(x^2 +1)))]_0 ^1 −∫_0 ^1 (x/(x+(√(x^2 +1)))).(1+(x/( (√(x^2 +1)))))dx =log((√2)+1)−(1/2)∫_0 ^1 ((2x)/( (√(x^2 +1)))) =log((√2)+1)−[(√(x^2 +1))]_0 ^1 =log((√2)+1)−(√2)+1=logy ⇒y=((√2)+1)e^(1−(√2))](https://www.tinkutara.com/question/Q115506.png)
$$\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\prod}}\left(\frac{\mathrm{r}}{\mathrm{n}}+\sqrt{\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }+\mathrm{1}}\overset{\frac{\mathrm{1}}{\mathrm{n}}} {\right)}=\mathrm{y} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\mathrm{log}\left(\frac{\mathrm{r}}{\mathrm{n}}+\sqrt{\frac{\mathrm{r}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }+\mathrm{1}}\right)=\mathrm{logy} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\mathrm{dx} \\ $$$$\left[\mathrm{xlog}\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}}{\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}.\left(\mathrm{1}+\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\right)\mathrm{dx} \\ $$$$=\mathrm{log}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$=\mathrm{log}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)−\left[\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{log}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)−\sqrt{\mathrm{2}}+\mathrm{1}=\mathrm{logy} \\ $$$$\Rightarrow\mathrm{y}=\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\mathrm{e}^{\mathrm{1}−\sqrt{\mathrm{2}}} \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 26/Sep/20
![let U_n =(1/n)(1+(√(1+n^2 )))^(1/n) .((√(2+(√(4+n^2 )))))^(1/n) ......((√(n+(√(n^2 +n^2 )))))^(1/n) ⇒ U_n =(1/n)(Π_(k=1) ^n (k+(√(k^2 +n^2 ))))^(1/n) = =(1/n){Π_(k=1) ^n (k+n(√((k^2 /n^2 )+1)))}^(1/n) =(1/n){n^n Π_(k=1) ^n ((k/n)+(√(1+((k/n))^2 )))}^(1/n) =(Π_(k=1) ^n ((k/n)+(√(1+((k/n))^2 )))^(1/n) ⇒ln(U_n ) =(1/n)Σ_(k=1) ^n ln((k/n)+(√(1+((k/n))^2 ))) ⇒lim_(n→+∞) ln(U_n ) =∫_0 ^1 ln(x+(√(1+x^2 )))dx we have ∫_0 ^1 ln(x+(√(1+x^2 )))dx =[xln(x+(√(1+x^2 )))]_0 ^1 −∫_0 ^1 x.(dx/( (√(1+x^2 )))) =ln(1+(√2))−[(√(1+x^2 ))]_0 ^1 =ln(1+(√2))−((√2)−1) ⇒lim_(n→+∞) U_n =e^(ln(1+(√2))+1−(√2)) =(1+(√2))e^(1−(√2)) =S](https://www.tinkutara.com/question/Q115509.png)
$$\mathrm{let}\:\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\left(\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{n}^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{n}}} .\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{4}+\mathrm{n}^{\mathrm{2}} }}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} ……\left(\sqrt{\mathrm{n}+\sqrt{\mathrm{n}^{\mathrm{2}} \:+\mathrm{n}^{\mathrm{2}} }}\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$\Rightarrow\:\mathrm{U}_{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{n}}\left(\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{k}+\sqrt{\mathrm{k}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} }\right)\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{n}}\left\{\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\mathrm{k}+\mathrm{n}\sqrt{\frac{\mathrm{k}^{\mathrm{2}} }{\mathrm{n}^{\mathrm{2}} }+\mathrm{1}}\right)\right\}^{\frac{\mathrm{1}}{\mathrm{n}}} \:=\frac{\mathrm{1}}{\mathrm{n}}\left\{\mathrm{n}^{\mathrm{n}} \:\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{k}}{\mathrm{n}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\right)\right\}^{\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$=\left(\prod_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{k}}{\mathrm{n}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\right)^{\frac{\mathrm{1}}{\mathrm{n}}} \:\Rightarrow\mathrm{ln}\left(\mathrm{U}_{\mathrm{n}} \right)\:=\frac{\mathrm{1}}{\mathrm{n}}\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \mathrm{ln}\left(\frac{\mathrm{k}}{\mathrm{n}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{k}}{\mathrm{n}}\right)^{\mathrm{2}} }\right)\right. \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{ln}\left(\mathrm{U}_{\mathrm{n}} \right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}\:\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\mathrm{dx}\:=\left[\mathrm{xln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}.\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }} \\ $$$$=\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\left[\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \:\:=\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{U}_{\mathrm{n}} =\mathrm{e}^{\mathrm{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\mathrm{1}−\sqrt{\mathrm{2}}} \:\:=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\mathrm{e}^{\mathrm{1}−\sqrt{\mathrm{2}}} \:\:=\mathrm{S} \\ $$$$ \\ $$
