Question Number 93005 by i jagooll last updated on 10/May/20
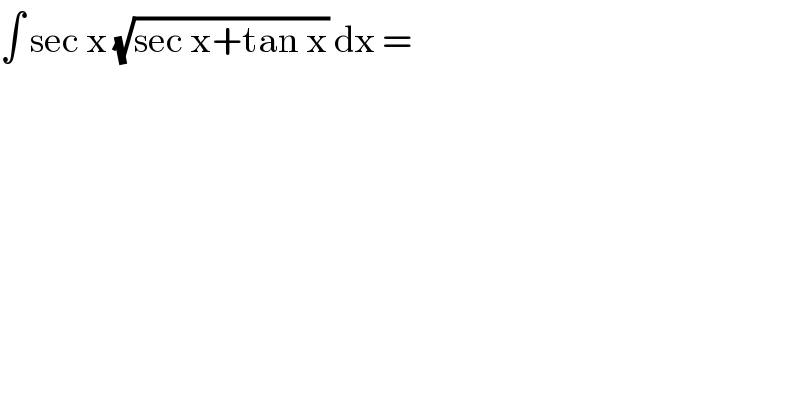
$$\int\:\mathrm{sec}\:\mathrm{x}\:\sqrt{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}\:=\: \\ $$
Answered by john santu last updated on 10/May/20
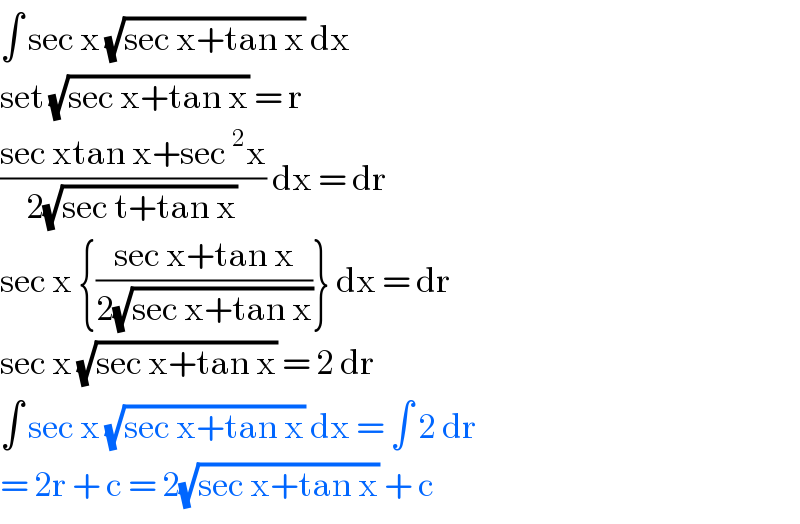
$$\int\:\mathrm{sec}\:\mathrm{x}\:\sqrt{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}\: \\ $$$$\mathrm{set}\:\sqrt{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\:=\:\mathrm{r}\: \\ $$$$\frac{\mathrm{sec}\:\mathrm{xtan}\:\mathrm{x}+\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{2}\sqrt{\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{x}}}\:\mathrm{dx}\:=\:\mathrm{dr} \\ $$$$\mathrm{sec}\:\mathrm{x}\:\left\{\frac{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}}\right\}\:\mathrm{dx}\:=\:\mathrm{dr} \\ $$$$\mathrm{sec}\:\mathrm{x}\:\sqrt{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\:=\:\mathrm{2}\:\mathrm{dr} \\ $$$$\int\:\mathrm{sec}\:\mathrm{x}\:\sqrt{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx}\:=\:\int\:\mathrm{2}\:\mathrm{dr} \\ $$$$=\:\mathrm{2r}\:+\:\mathrm{c}\:=\:\mathrm{2}\sqrt{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\:+\:\mathrm{c}\: \\ $$
Commented by i jagooll last updated on 10/May/20

$$\mathrm{thanks}\: \\ $$
