Question Number 151568 by tabata last updated on 21/Aug/21

$$\int\:\sqrt{{sec}\left({x}\right)+{tan}\left({x}\right)}\:{dx} \\ $$$$ \\ $$$${how}\:{can}\:{it}\:{solve} \\ $$
Answered by puissant last updated on 22/Aug/21
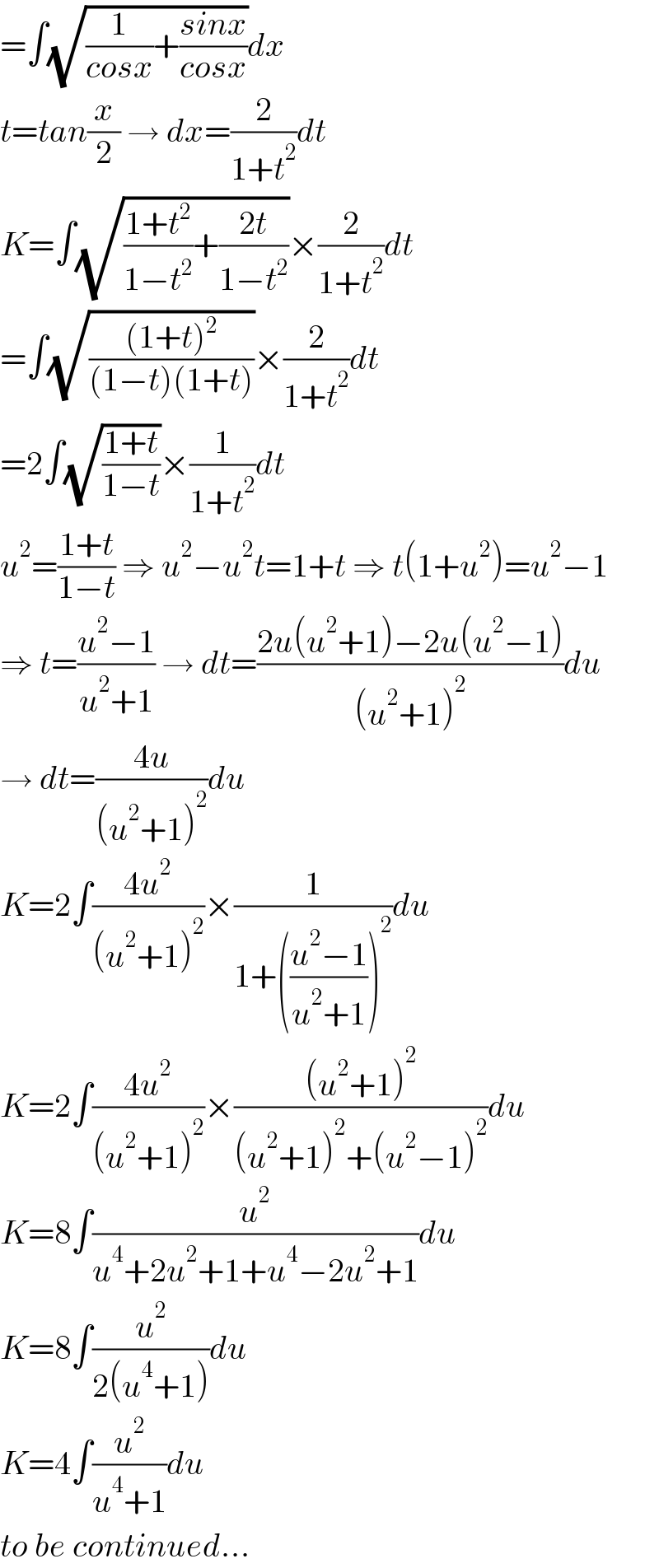
$$=\int\sqrt{\frac{\mathrm{1}}{{cosx}}+\frac{{sinx}}{{cosx}}}{dx} \\ $$$${t}={tan}\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${K}=\int\sqrt{\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\int\sqrt{\frac{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)}}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{2}\int\sqrt{\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}}×\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${u}^{\mathrm{2}} =\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\:\Rightarrow\:{u}^{\mathrm{2}} −{u}^{\mathrm{2}} {t}=\mathrm{1}+{t}\:\Rightarrow\:{t}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)={u}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\:{t}=\frac{{u}^{\mathrm{2}} −\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}\:\rightarrow\:{dt}=\frac{\mathrm{2}{u}\left({u}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{2}{u}\left({u}^{\mathrm{2}} −\mathrm{1}\right)}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$\rightarrow\:{dt}=\frac{\mathrm{4}{u}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$${K}=\mathrm{2}\int\frac{\mathrm{4}{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{u}^{\mathrm{2}} −\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }{du} \\ $$$${K}=\mathrm{2}\int\frac{\mathrm{4}{u}^{\mathrm{2}} }{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }×\frac{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} +\left({u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$${K}=\mathrm{8}\int\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} +\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}+{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} +\mathrm{1}}{du} \\ $$$${K}=\mathrm{8}\int\frac{{u}^{\mathrm{2}} }{\mathrm{2}\left({u}^{\mathrm{4}} +\mathrm{1}\right)}{du} \\ $$$${K}=\mathrm{4}\int\frac{{u}^{\mathrm{2}} }{{u}^{\mathrm{4}} +\mathrm{1}}{du} \\ $$$${to}\:{be}\:{continued}… \\ $$
Commented by peter frank last updated on 22/Aug/21
![4∫.(1/2). ((2u^2 )/(1+u^4 ))=2∫((2u^2 )/(1+u^4 )) 2∫((2u^2 )/(1+u^4 ))=4∫(((u^2 +1)+(u^2 −1))/(1+u^4 ))du 4[∫((1+u^2 )/(1+u^4 ))du+∫((1−u^2 )/(1+u^4 ))du] 4[∫((1+(1/u^2 ))/((u−(1/u))^2 +2))+∫((1−(1/u^2 ))/((u+(1/u))^2 +2)) t=u−(1/u) dt=(1+(1/u^2 ))du x=u+(1/u) dx=(1−(1/u^2 ))du 4[∫(1/2).(dt/(t^2 +2))+∫(1/2).∫(dx/(x^2 −2)) 2[(1/( (√2)))tan^(−1) ((t/( (√2))))+(1/(2(√2)))ln (((x−(√2))/(x+(√2))))](https://www.tinkutara.com/question/Q151583.png)
$$\mathrm{4}\int.\frac{\mathrm{1}}{\mathrm{2}}.\:\:\frac{\mathrm{2u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{4}} }=\mathrm{2}\int\frac{\mathrm{2u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{4}} } \\ $$$$\mathrm{2}\int\frac{\mathrm{2u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{4}} }=\mathrm{4}\int\frac{\left(\mathrm{u}^{\mathrm{2}} +\mathrm{1}\right)+\left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{1}+\mathrm{u}^{\mathrm{4}} }\mathrm{du} \\ $$$$\mathrm{4}\left[\int\frac{\mathrm{1}+\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{4}} }\mathrm{du}+\int\frac{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }{\mathrm{1}+\mathrm{u}^{\mathrm{4}} }\mathrm{du}\right] \\ $$$$\mathrm{4}\left[\int\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} +\mathrm{2}}+\int\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\right)^{\mathrm{2}} +\mathrm{2}}\right. \\ $$$$\mathrm{t}=\mathrm{u}−\frac{\mathrm{1}}{\mathrm{u}} \\ $$$$\mathrm{dt}=\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)\mathrm{du} \\ $$$$\mathrm{x}=\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}} \\ $$$$\mathrm{dx}=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)\mathrm{du} \\ $$$$\mathrm{4}\left[\int\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{2}}+\int\frac{\mathrm{1}}{\mathrm{2}}.\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} −\mathrm{2}}\right. \\ $$$$\mathrm{2}\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{t}}{\:\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\:\left(\frac{\mathrm{x}−\sqrt{\mathrm{2}}}{\mathrm{x}+\sqrt{\mathrm{2}}}\right)\right. \\ $$$$ \\ $$
Answered by peter frank last updated on 22/Aug/21
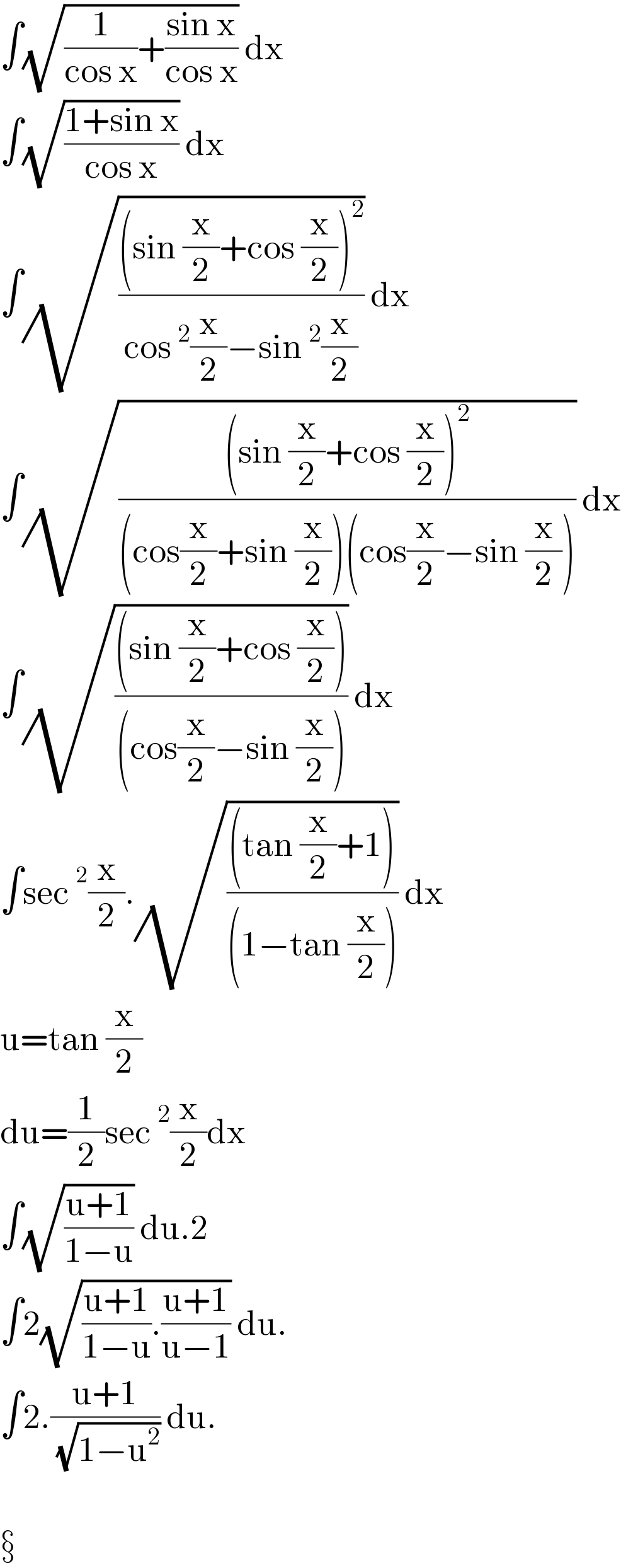
$$\int\sqrt{\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{x}}+\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}}\:\mathrm{dx} \\ $$$$\int\sqrt{\frac{\mathrm{1}+\mathrm{sin}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}}}\:\mathrm{dx} \\ $$$$\int\sqrt{\frac{\left(\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}}\:\mathrm{dx} \\ $$$$\int\sqrt{\frac{\left(\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left(\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)\left(\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)}}\:\mathrm{dx} \\ $$$$\int\sqrt{\frac{\left(\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}\right)}{\left(\mathrm{cos}\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}\right)}}\:\mathrm{dx} \\ $$$$\int\mathrm{sec}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}.\sqrt{\frac{\left(\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{1}\right)}{\left(\mathrm{1}−\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\right)}}\:\mathrm{dx} \\ $$$$\mathrm{u}=\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}} \\ $$$$\mathrm{du}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\mathrm{dx} \\ $$$$\int\sqrt{\frac{\mathrm{u}+\mathrm{1}}{\mathrm{1}−\mathrm{u}}}\:\mathrm{du}.\mathrm{2} \\ $$$$\int\mathrm{2}\sqrt{\frac{\mathrm{u}+\mathrm{1}}{\mathrm{1}−\mathrm{u}}.\frac{\mathrm{u}+\mathrm{1}}{\mathrm{u}−\mathrm{1}}}\:\mathrm{du}. \\ $$$$\int\mathrm{2}.\frac{\mathrm{u}+\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }}\:\mathrm{du}. \\ $$$$ \\ $$$$ \\ $$
Commented by talminator2856791 last updated on 22/Aug/21
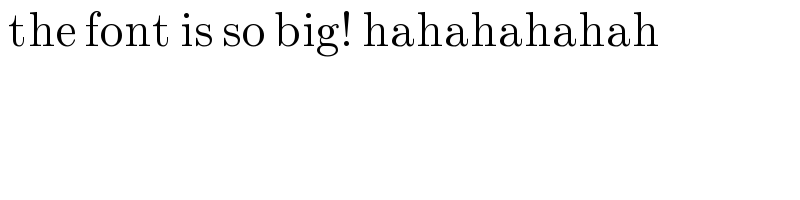
$$\:\mathrm{the}\:\mathrm{font}\:\mathrm{is}\:\mathrm{so}\:\mathrm{big}!\:\mathrm{hahahahahah} \\ $$
Answered by MJS_new last updated on 22/Aug/21
![∫(√(sec x +tan x)) dx= [t=tan (x/2) → dx=((2dt)/(1+t^2 ))] =2∫((√(1+t))/((1+t^2 )(√(1−t))))dt= [u=((√(1−t))/( (√(1+t)))) → dt=−(√((1−t)(1+t)^3 )) du] =−4∫(du/(u^4 +1))= =(1/( (√2)))∫((2u−(√2))/(u^2 −(√2)u+1))du−∫(du/(u^2 −(√2)u+1))− −(1/( (√2)))∫((2u+(√2))/(u^2 +(√2)u+1))du−∫(du/(u^2 +(√2)u+1))= =((√2)/2)ln (u^2 −(√2)u+1) −(√2)arctan ((√2)u−1) − +((√2)/2)ln (u^2 +(√2)u+1) −(√2)arctan ((√2)u+1) ...](https://www.tinkutara.com/question/Q151584.png)
$$\int\sqrt{\mathrm{sec}\:{x}\:+\mathrm{tan}\:{x}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\right] \\ $$$$=\mathrm{2}\int\frac{\sqrt{\mathrm{1}+{t}}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}−{t}}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{1}−{t}}}{\:\sqrt{\mathrm{1}+{t}}}\:\rightarrow\:{dt}=−\sqrt{\left(\mathrm{1}−{t}\right)\left(\mathrm{1}+{t}\right)^{\mathrm{3}} }\:{du}\right] \\ $$$$=−\mathrm{4}\int\frac{{du}}{{u}^{\mathrm{4}} +\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\mathrm{2}{u}−\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}}{du}−\int\frac{{du}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}}− \\ $$$$\:\:\:\:\:−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\int\frac{\mathrm{2}{u}+\sqrt{\mathrm{2}}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}{du}−\int\frac{{du}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\left({u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}\right)\:−\sqrt{\mathrm{2}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{u}−\mathrm{1}\right)\:− \\ $$$$\:\:\:\:\:+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\left({u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}\right)\:−\sqrt{\mathrm{2}}\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{u}+\mathrm{1}\right) \\ $$$$… \\ $$
Commented by peter frank last updated on 22/Aug/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Ar Brandon last updated on 22/Aug/21

$${I}=\int\sqrt{\mathrm{sec}{x}+\mathrm{tan}{x}}{dx}=\int\sqrt{\frac{\mathrm{1}+\mathrm{sin}{x}}{\mathrm{cos}{x}}}{dx} \\ $$$$\:\:=\int\sqrt{\frac{\left(\mathrm{cos}\frac{{x}}{\mathrm{2}}+\mathrm{sin}\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{cos}{x}}}{dx}=\int\frac{\mathrm{cos}\frac{{x}}{\mathrm{2}}+\mathrm{sin}\frac{{x}}{\mathrm{2}}}{\:\sqrt{\mathrm{cos}{x}}}{dx} \\ $$$$\:\:=\int\frac{\mathrm{cos}\frac{{x}}{\mathrm{2}}}{\:\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}}{dx}+\int\frac{\mathrm{sin}\frac{{x}}{\mathrm{2}}}{\:\sqrt{\mathrm{2cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{1}}}{dx} \\ $$$$\:\:=\sqrt{\mathrm{2}}\mathrm{arcsin}\left(\sqrt{\mathrm{2}}\mathrm{sin}\frac{{x}}{\mathrm{2}}\right)−\sqrt{\mathrm{2}}\mathrm{argcosh}\left(\sqrt{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}}\right)+{C} \\ $$$$\:\:=\sqrt{\mathrm{2}}\mathrm{arcsin}\left(\sqrt{\mathrm{2}}\mathrm{sin}\frac{{x}}{\mathrm{2}}\right)−\sqrt{\mathrm{2}}\mathrm{ln}\mid\sqrt{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}}+\sqrt{\mathrm{2cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{1}}\mid+{C} \\ $$
Commented by peter frank last updated on 22/Aug/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
