secx-dx-

Question Number 147867 by Khalmohmmad last updated on 24/Jul/21

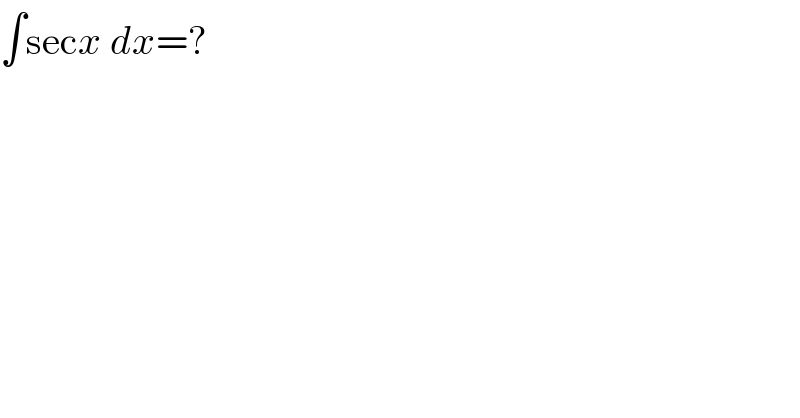
$$\int\mathrm{sec}{x}\:{dx}=? \\ $$

Answered by Olaf_Thorendsen last updated on 24/Jul/21

F(x) = ∫secx dx F(x) = ∫(dx/(cosx)) Let t = tan(x/2) F(t) = ∫(1/((1−t^2 )/(1+t^2 ))).((2dt)/(1+t^2 )) F(t) = ∫((1/(1−t))+(1/(1+t))) dt F(t) = ln∣((1+t)/(1−t))∣+C F(x) = ln∣((1+tan(x/2))/(1−tan(x/2)))∣+C F(x) = ln∣((cos(x/2)+sin(x/2))/(cos(x/2)−sin(x/2)))∣+C F(x) = ln∣(((√2)cos((π/4)−(x/2)))/( (√2)sin((π/4)−(x/2))))∣+C F(x) = ln∣cot((π/4)−(x/2))∣+C

$$\mathrm{F}\left({x}\right)\:=\:\int\mathrm{sec}{x}\:{dx} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\int\frac{{dx}}{\mathrm{cos}{x}} \\ $$$$\mathrm{Let}\:{t}\:=\:\mathrm{tan}\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{F}\left({t}\right)\:=\:\int\frac{\mathrm{1}}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\mathrm{F}\left({t}\right)\:=\:\int\left(\frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)\:{dt} \\ $$$$\mathrm{F}\left({t}\right)\:=\:\mathrm{ln}\mid\frac{\mathrm{1}+{t}}{\mathrm{1}−{t}}\mid+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{ln}\mid\frac{\mathrm{1}+\mathrm{tan}\frac{{x}}{\mathrm{2}}}{\mathrm{1}−\mathrm{tan}\frac{{x}}{\mathrm{2}}}\mid+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{ln}\mid\frac{\mathrm{cos}\frac{{x}}{\mathrm{2}}+\mathrm{sin}\frac{{x}}{\mathrm{2}}}{\mathrm{cos}\frac{{x}}{\mathrm{2}}−\mathrm{sin}\frac{{x}}{\mathrm{2}}}\mid+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}\mathrm{cos}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}{\:\sqrt{\mathrm{2}}\mathrm{sin}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)}\mid+\mathrm{C} \\ $$$$\mathrm{F}\left({x}\right)\:=\:\mathrm{ln}\mid\mathrm{cot}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\mid+\mathrm{C} \\ $$

Answered by puissant last updated on 24/Jul/21

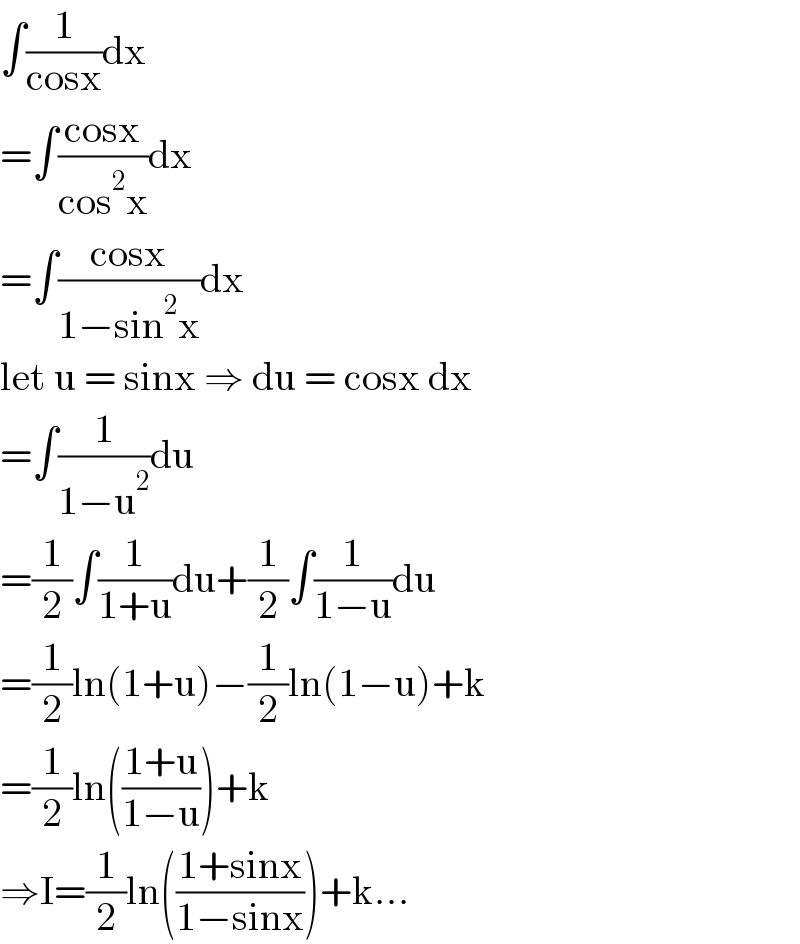
∫(1/(cosx))dx =∫((cosx)/(cos^2 x))dx =∫((cosx)/(1−sin^2 x))dx let u = sinx ⇒ du = cosx dx =∫(1/(1−u^2 ))du =(1/2)∫(1/(1+u))du+(1/2)∫(1/(1−u))du =(1/2)ln(1+u)−(1/2)ln(1−u)+k =(1/2)ln(((1+u)/(1−u)))+k ⇒I=(1/2)ln(((1+sinx)/(1−sinx)))+k...

$$\int\frac{\mathrm{1}}{\mathrm{cosx}}\mathrm{dx} \\ $$$$=\int\frac{\mathrm{cosx}}{\mathrm{cos}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$=\int\frac{\mathrm{cosx}}{\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{u}\:=\:\mathrm{sinx}\:\Rightarrow\:\mathrm{du}\:=\:\mathrm{cosx}\:\mathrm{dx} \\ $$$$=\int\frac{\mathrm{1}}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\mathrm{du}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{\mathrm{1}−\mathrm{u}}\mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{1}−\mathrm{u}\right)+\mathrm{k} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{u}}{\mathrm{1}−\mathrm{u}}\right)+\mathrm{k} \\ $$$$\Rightarrow\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\mathrm{1}+\mathrm{sinx}}{\mathrm{1}−\mathrm{sinx}}\right)+\mathrm{k}… \\ $$

Answered by iloveisrael last updated on 24/Jul/21

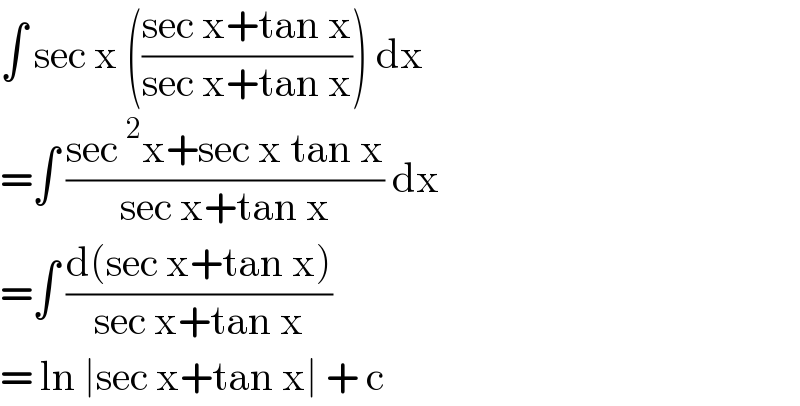
∫ sec x (((sec x+tan x)/(sec x+tan x))) dx =∫ ((sec^2 x+sec x tan x)/(sec x+tan x)) dx =∫ ((d(sec x+tan x))/(sec x+tan x)) = ln ∣sec x+tan x∣ + c

$$\int\:\mathrm{sec}\:\mathrm{x}\:\left(\frac{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\right)\:\mathrm{dx} \\ $$$$=\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sec}\:\mathrm{x}\:\mathrm{tan}\:\mathrm{x}}{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}}\:\mathrm{dx} \\ $$$$=\int\:\frac{\mathrm{d}\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}} \\ $$$$=\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\mid\:+\:\mathrm{c}\: \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply