Question Number 106743 by mohammad17 last updated on 06/Aug/20

$$\int\sqrt{{secy}}{dy} \\ $$
Answered by Sarah85 last updated on 07/Aug/20
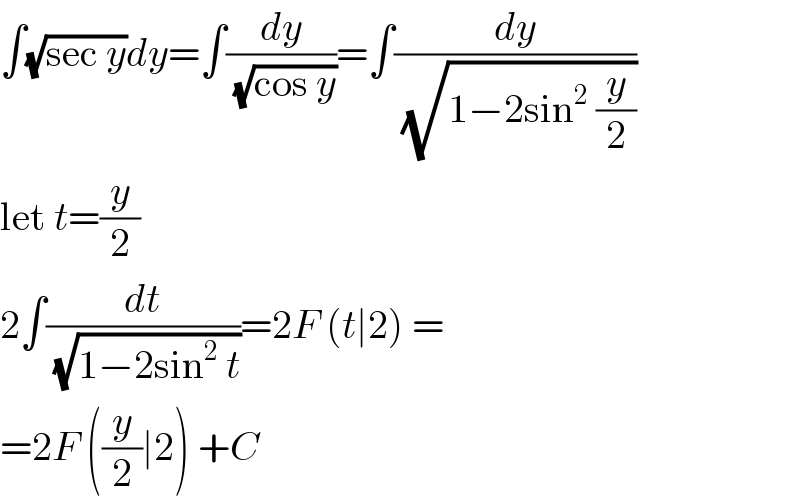
$$\int\sqrt{\mathrm{sec}\:{y}}{dy}=\int\frac{{dy}}{\:\sqrt{\mathrm{cos}\:{y}}}=\int\frac{{dy}}{\:\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:\frac{{y}}{\mathrm{2}}}} \\ $$$$\mathrm{let}\:{t}=\frac{{y}}{\mathrm{2}} \\ $$$$\mathrm{2}\int\frac{{dt}}{\:\sqrt{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \:{t}}}=\mathrm{2}{F}\:\left({t}\mid\mathrm{2}\right)\:= \\ $$$$=\mathrm{2}{F}\:\left(\frac{{y}}{\mathrm{2}}\mid\mathrm{2}\right)\:+{C} \\ $$
Commented by Her_Majesty last updated on 07/Aug/20
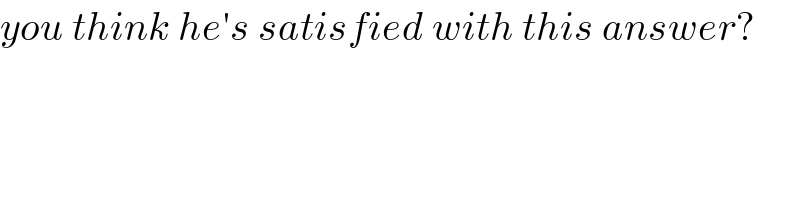
$${you}\:{think}\:{he}'{s}\:{satisfied}\:{with}\:{this}\:{answer}? \\ $$
Commented by Sarah85 last updated on 07/Aug/20
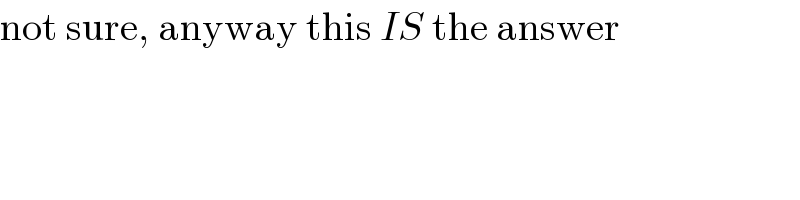
$$\mathrm{not}\:\mathrm{sure},\:\mathrm{anyway}\:\mathrm{this}\:{IS}\:\mathrm{the}\:\mathrm{answer} \\ $$
