Menu Close

Show-by-recurence-that-5-n-1-4n-n-N-

Tinku Tara 0 Comments
Pin




Question Number 119054 by mathocean1 last updated on 21/Oct/20
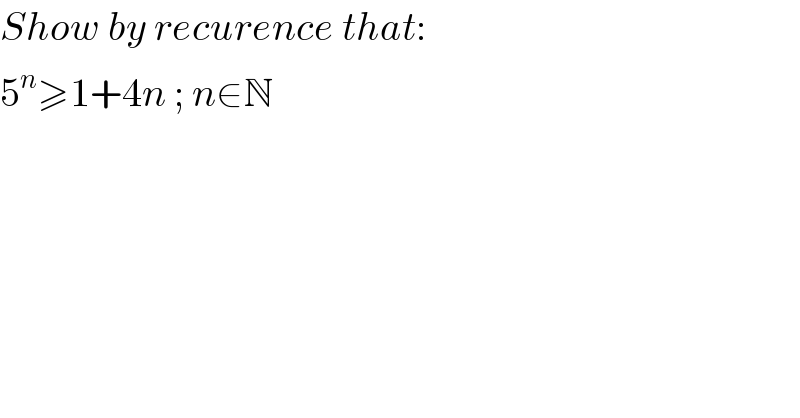
Show by recurence that: 5^n ≥1+4n ; n∈N
Showbyrecurencethat:5n⩾1+4n;n∈N
Answered by 1549442205PVT last updated on 22/Oct/20
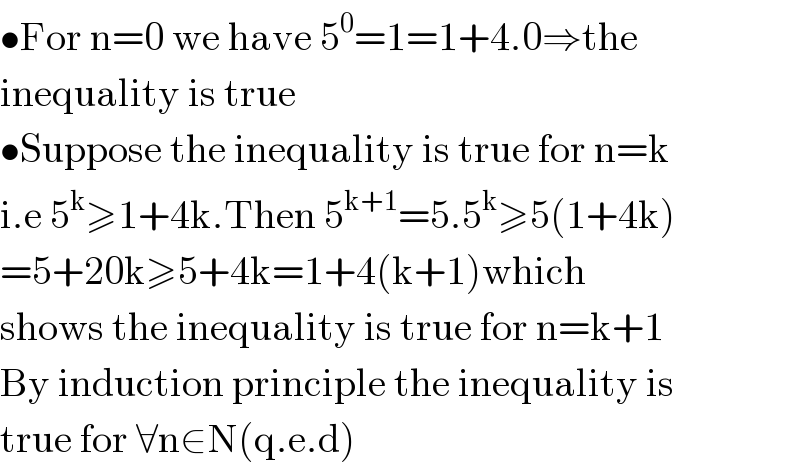
•For n=0 we have 5^0 =1=1+4.0⇒the inequality is true •Suppose the inequality is true for n=k i.e 5^k ≥1+4k.Then 5^(k+1) =5.5^k ≥5(1+4k) =5+20k≥5+4k=1+4(k+1)which shows the inequality is true for n=k+1 By induction principle the inequality is true for ∀n∈N(q.e.d)
∙Forn=0wehave50=1=1+4.0⇒theinequalityistrue∙Supposetheinequalityistrueforn=ki.e5k⩾1+4k.Then5k+1=5.5k⩾5(1+4k)=5+20k⩾5+4k=1+4(k+1)whichshowstheinequalityistrueforn=k+1Byinductionprincipletheinequalityistruefor∀n∈N(q.e.d)
Answered by Bird last updated on 21/Oct/20
n=0 we get 1≥1+0 (true) let suppose 5^n ≥1+4n and prove 5^(n+1) ≥1+4(n+1) we hsve 5^n ≥1+4n(hypothese) ⇒ 5^(n+1) ≥5(1+4n)=5+20n we have 5+20n−(1+4(n+1)) =5+20n−5−4n =16n≥0 ⇒ 5^(n+1) ≥1+4(n+1) so the relation is true at term n+1
n=0weget1⩾1+0(true)letsuppose5n⩾1+4nandprove5n+1⩾1+4(n+1)wehsve5n⩾1+4n(hypothese)⇒5n+1⩾5(1+4n)=5+20nwehave5+20n−(1+4(n+1))=5+20n−5−4n=16n⩾0⇒5n+1⩾1+4(n+1)sotherelationistrueattermn+1

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *