Menu Close

Show-by-recurence-that-n-N-k-1-n-1-k-k-1-k-2-n-n-3-4-n-1-n-2-

Tinku Tara 0 Comments
Pin




Question Number 119055 by mathocean1 last updated on 21/Oct/20
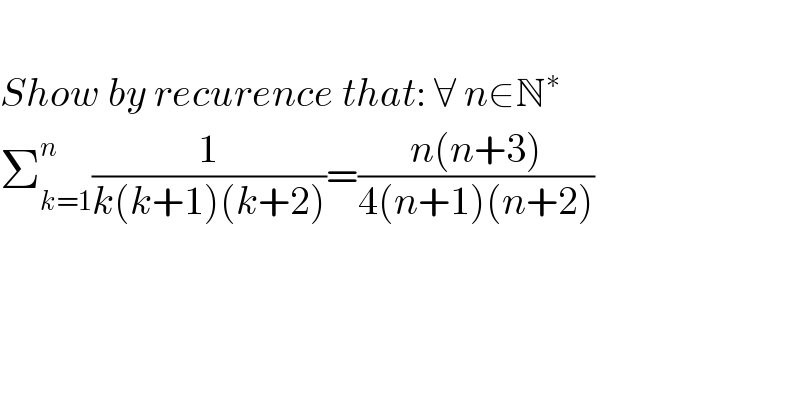
Show by recurence that: ∀ n∈N^∗ Σ_(k=1) ^n (1/(k(k+1)(k+2)))=((n(n+3))/(4(n+1)(n+2)))
$$ \\ $$$${Show}\:{by}\:{recurence}\:{that}:\:\forall\:{n}\in\mathbb{N}^{\ast} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}=\frac{{n}\left({n}+\mathrm{3}\right)}{\mathrm{4}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$
Answered by Bird last updated on 21/Oct/20
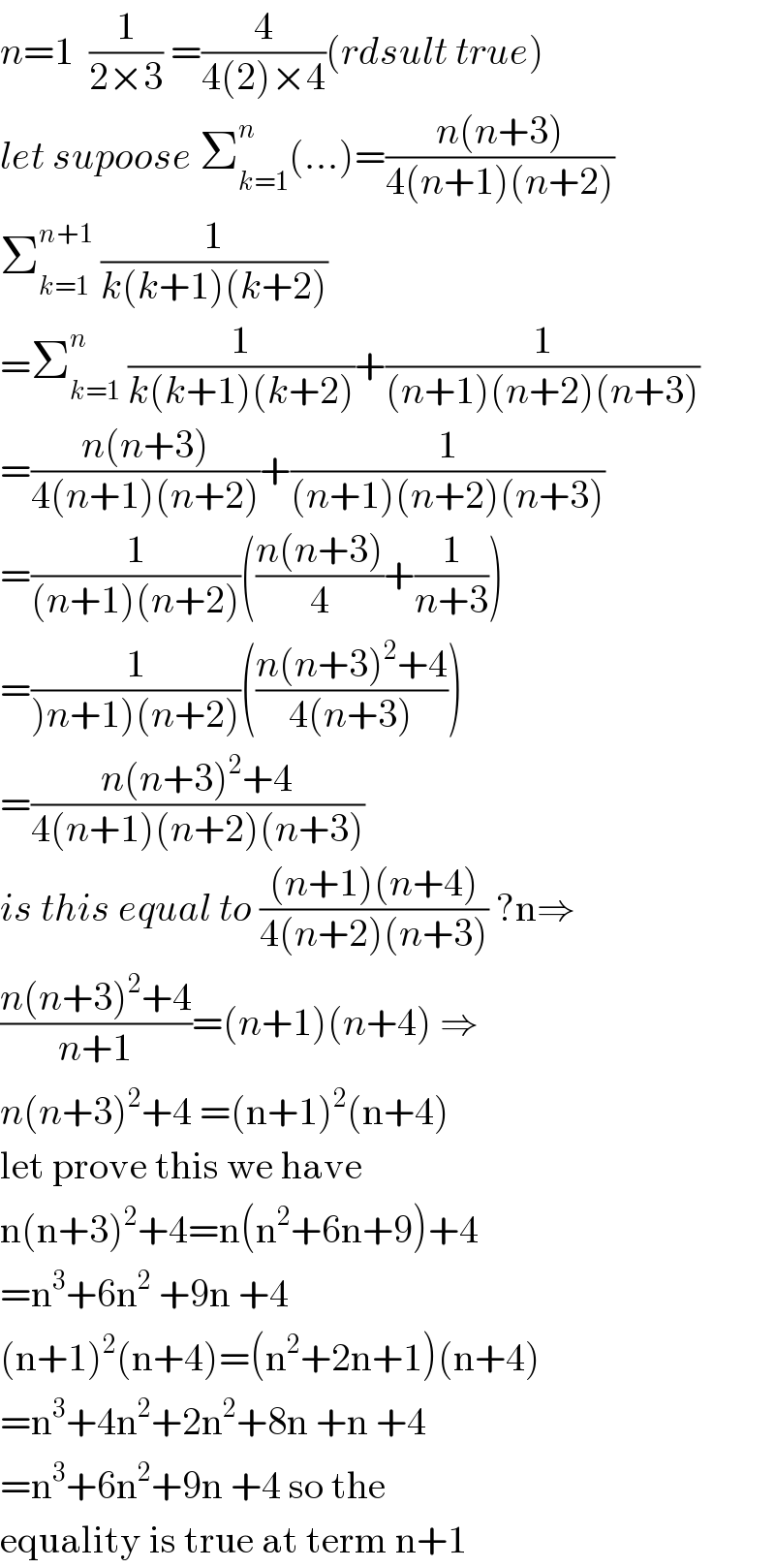
n=1 (1/(2×3)) =(4/(4(2)×4))(rdsult true) let supoose Σ_(k=1) ^(n ) (...)=((n(n+3))/(4(n+1)(n+2))) Σ_(k=1) ^(n+1) (1/(k(k+1)(k+2))) =Σ_(k=1) ^n (1/(k(k+1)(k+2)))+(1/((n+1)(n+2)(n+3))) =((n(n+3))/(4(n+1)(n+2)))+(1/((n+1)(n+2)(n+3))) =(1/((n+1)(n+2)))(((n(n+3))/4)+(1/(n+3))) =(1/()n+1)(n+2)))(((n(n+3)^2 +4)/(4(n+3)))) =((n(n+3)^2 +4)/(4(n+1)(n+2)(n+3))) is this equal to (((n+1)(n+4))/(4(n+2)(n+3))) ?n⇒ ((n(n+3)^2 +4)/(n+1))=(n+1)(n+4) ⇒ n(n+3)^2 +4 =(n+1)^2 (n+4) let prove this we have n(n+3)^2 +4=n(n^2 +6n+9)+4 =n^3 +6n^2 +9n +4 (n+1)^2 (n+4)=(n^2 +2n+1)(n+4) =n^3 +4n^2 +2n^2 +8n +n +4 =n^3 +6n^2 +9n +4 so the equality is true at term n+1
$${n}=\mathrm{1}\:\:\frac{\mathrm{1}}{\mathrm{2}×\mathrm{3}}\:=\frac{\mathrm{4}}{\mathrm{4}\left(\mathrm{2}\right)×\mathrm{4}}\left({rdsult}\:{true}\right) \\ $$$${let}\:{supoose}\:\sum_{{k}=\mathrm{1}} ^{{n}\:} \left(…\right)=\frac{{n}\left({n}+\mathrm{3}\right)}{\mathrm{4}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$$$=\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$$=\frac{{n}\left({n}+\mathrm{3}\right)}{\mathrm{4}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\left(\frac{{n}\left({n}+\mathrm{3}\right)}{\mathrm{4}}+\frac{\mathrm{1}}{{n}+\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\left.\right)\left.{n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\left(\frac{{n}\left({n}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4}}{\mathrm{4}\left({n}+\mathrm{3}\right)}\right) \\ $$$$=\frac{{n}\left({n}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4}}{\mathrm{4}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)} \\ $$$${is}\:{this}\:{equal}\:{to}\:\frac{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{4}\right)}{\mathrm{4}\left({n}+\mathrm{2}\right)\left({n}+\mathrm{3}\right)}\:?\mathrm{n}\Rightarrow \\ $$$$\frac{{n}\left({n}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4}}{{n}+\mathrm{1}}=\left({n}+\mathrm{1}\right)\left({n}+\mathrm{4}\right)\:\Rightarrow \\ $$$${n}\left({n}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4}\:=\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{n}+\mathrm{4}\right) \\ $$$$\mathrm{let}\:\mathrm{prove}\:\mathrm{this}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{n}\left(\mathrm{n}+\mathrm{3}\right)^{\mathrm{2}} +\mathrm{4}=\mathrm{n}\left(\mathrm{n}^{\mathrm{2}} +\mathrm{6n}+\mathrm{9}\right)+\mathrm{4} \\ $$$$=\mathrm{n}^{\mathrm{3}} +\mathrm{6n}^{\mathrm{2}} \:+\mathrm{9n}\:+\mathrm{4} \\ $$$$\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{n}+\mathrm{4}\right)=\left(\mathrm{n}^{\mathrm{2}} +\mathrm{2n}+\mathrm{1}\right)\left(\mathrm{n}+\mathrm{4}\right) \\ $$$$=\mathrm{n}^{\mathrm{3}} +\mathrm{4n}^{\mathrm{2}} +\mathrm{2n}^{\mathrm{2}} +\mathrm{8n}\:+\mathrm{n}\:+\mathrm{4} \\ $$$$=\mathrm{n}^{\mathrm{3}} +\mathrm{6n}^{\mathrm{2}} +\mathrm{9n}\:+\mathrm{4}\:\mathrm{so}\:\mathrm{the}\: \\ $$$$\mathrm{equality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{at}\:\mathrm{term}\:\mathrm{n}+\mathrm{1} \\ $$
Answered by Dwaipayan Shikari last updated on 22/Oct/20
Without Induction Σ_(k=1) ^n (1/(k(k+1)(k+2))) =(1/2)Σ_(k=1) ^n ((k+2−k)/(k(k+1)(k+2))) =(1/2)Σ_(k=1) ^n (1/(k(k+1)))−(1/((k+1)(k+2))) =(1/2)Σ_(k=1) ^n (1/k)−(1/(k+1))−(1/2)Σ_(k=1) ^n (1/(k+1))−(1/(k+2)) =(1/2)(1−(1/(n+1)))−(1/2)((1/2)−(1/(n+2))) =((2n(n+2)−n(n+1))/(4(n+1)(n+2)))=((n(n+3))/(4(n+1)(n+2)))
$${Without}\:{Induction} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}+\mathrm{2}−{k}}{{k}\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}\left({k}+\mathrm{1}\right)}−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)\left({k}+\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}−\frac{\mathrm{1}}{{k}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{1}}−\frac{\mathrm{1}}{{k}+\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{2}{n}\left({n}+\mathrm{2}\right)−{n}\left({n}+\mathrm{1}\right)}{\mathrm{4}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}=\frac{{n}\left({n}+\mathrm{3}\right)}{\mathrm{4}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *