Question Number 157254 by physicstutes last updated on 21/Oct/21
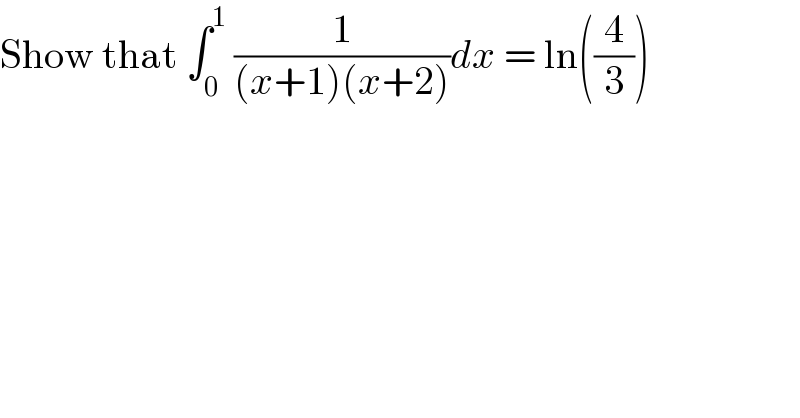
$$\mathrm{Show}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}{dx}\:=\:\mathrm{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right) \\ $$
Answered by puissant last updated on 21/Oct/21
![Ω=∫_0 ^1 (1/((x+1)(x+2)))dx = ∫_0 ^1 {(1/(x+1))−(1/(x+2))}dx =[ln(((x+1)/(x+2)))]_0 ^1 = ln((2/3))+ln2=2ln2−ln3 = ln((4/3))..](https://www.tinkutara.com/question/Q157259.png)
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{2}}\right\}{dx} \\ $$$$=\left[{ln}\left(\frac{{x}+\mathrm{1}}{{x}+\mathrm{2}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\:{ln}\left(\frac{\mathrm{2}}{\mathrm{3}}\right)+{ln}\mathrm{2}=\mathrm{2}{ln}\mathrm{2}−{ln}\mathrm{3} \\ $$$$=\:{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right).. \\ $$
