Question Number 126065 by Lordose last updated on 17/Dec/20
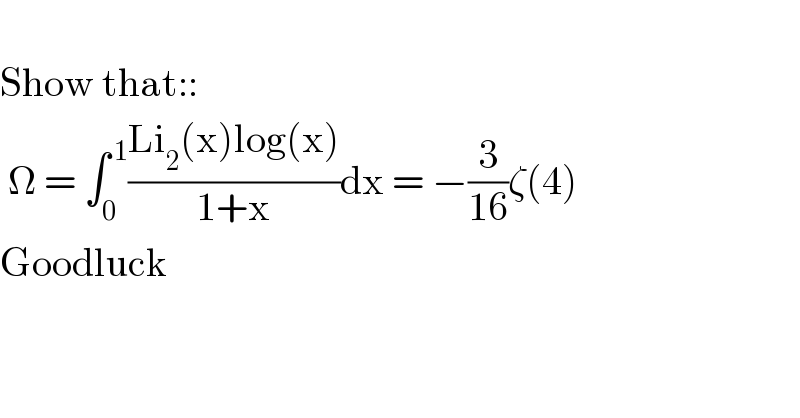
$$ \\ $$$$\mathrm{Show}\:\mathrm{that}:: \\ $$$$\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{log}\left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:=\:−\frac{\mathrm{3}}{\mathrm{16}}\zeta\left(\mathrm{4}\right) \\ $$$$\mathrm{Goodluck} \\ $$
Answered by mnjuly1970 last updated on 17/Dec/20

$$\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}^{\mathrm{2}} }\right)\frac{{log}\left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$\:\:\:=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{{n}} {log}\left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$\:\:\:=\underset{{n}=} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{{log}\left({x}\right)\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{m}} {x}^{{n}+{m}} \right\}{dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\underset{{m}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{m}+\mathrm{1}} \frac{\mathrm{1}}{\left({n}+{m}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}} }{\left({n}+{m}\right)^{\mathrm{2}} {n}^{\mathrm{2}} } \\ $$$$\underset{{property}} {\overset{{symmetrey}} {=}}\:\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{m}={n}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}−{n}} }{\left({mn}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} }\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{−\pi^{\mathrm{2}} }{\mathrm{12}}\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{\mathrm{2}}\:\ast\frac{\pi^{\mathrm{4}} }{\mathrm{144}} \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\ast\frac{\mathrm{90}}{\mathrm{144}}\zeta\left(\mathrm{4}\right)=−\frac{\mathrm{15}}{\mathrm{48}}\zeta\left(\mathrm{4}\right)=−\frac{\mathrm{3}}{\mathrm{16}}\zeta\left(\mathrm{4}\right)\checkmark \\ $$$$ \\ $$$$\:\:\:\: \\ $$
