Question Number 89286 by M±th+et£s last updated on 16/Apr/20
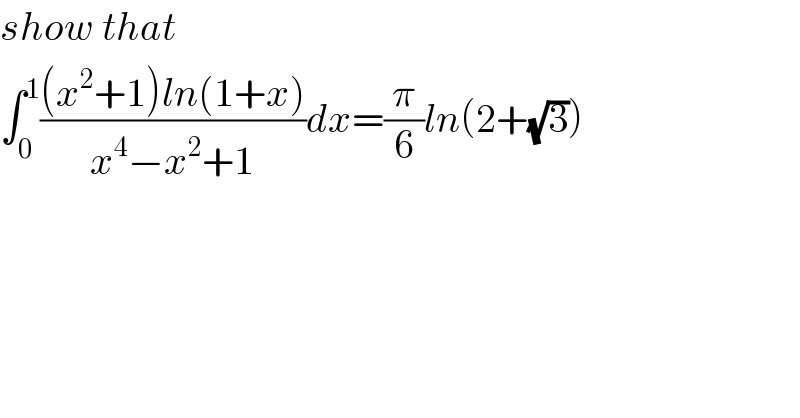
$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\pi}{\mathrm{6}}{ln}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$
Answered by TANMAY PANACEA. last updated on 16/Apr/20
![∫((1+(1/x^2 ))/(x^2 +(1/x^2 )−1)).ln(1+x)dx ln(1+x)∫((d(x−(1/x))^ )/((x−(1/x))^2 +1))−∫[(1/(1+x))∫((d(x−(1/x)))/((x−(1/x))^2 +1))dx]dx ln(1+x).tan^(−1) (x−(1/x))−∫((tan^(−1) (x−(1/x)))/(1+x))dx wait...](https://www.tinkutara.com/question/Q89296.png)
$$\int\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\mathrm{1}}.{ln}\left(\mathrm{1}+{x}\right){dx} \\ $$$${ln}\left(\mathrm{1}+{x}\right)\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)^{} }{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}}−\int\left[\frac{\mathrm{1}}{\mathrm{1}+{x}}\int\frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{1}}{dx}\right]{dx} \\ $$$${ln}\left(\mathrm{1}+{x}\right).{tan}^{−\mathrm{1}} \left({x}−\frac{\mathrm{1}}{{x}}\right)−\int\frac{{tan}^{−\mathrm{1}} \left({x}−\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}+{x}}{dx} \\ $$$${wait}… \\ $$
Commented by M±th+et£s last updated on 16/Apr/20

$${ok}\:{sir}\: \\ $$
Answered by M±th+et£s last updated on 16/Apr/20

