Question Number 80397 by M±th+et£s last updated on 02/Feb/20
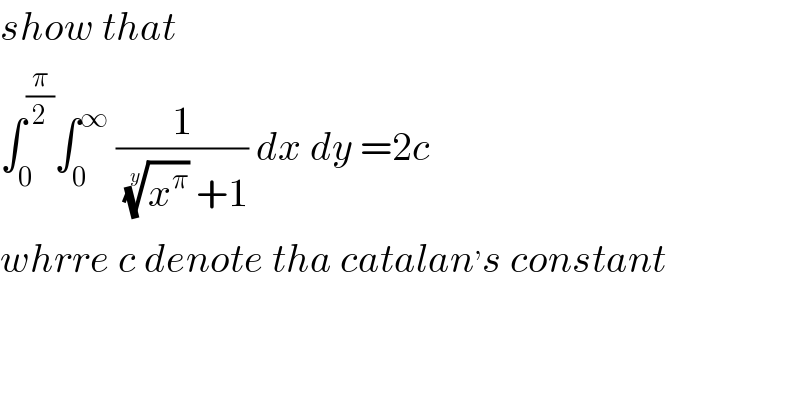
$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\:\sqrt[{{y}}]{{x}^{\pi} }\:+\mathrm{1}}\:{dx}\:{dy}\:=\mathrm{2}{c}\: \\ $$$${whrre}\:{c}\:{denote}\:{tha}\:{catalan}^{,} {s}\:{constant} \\ $$
Commented by mathmax by abdo last updated on 02/Feb/20

$${vhangement}\:^{{y}} \sqrt{{x}^{\pi} }={t}\:{give}\:\:{x}={t}^{\frac{{y}}{\pi}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left(^{{y}} \sqrt{{x}^{\pi} }\right)+\mathrm{1}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{y}}{\pi}{t}^{\frac{{y}}{\pi}−\mathrm{1}} ×\frac{{dt}}{{t}+\mathrm{1}}\:=\frac{{y}}{\pi}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{{y}}{\pi}−\mathrm{1}} }{{t}+\mathrm{1}}{dt} \\ $$$$=\frac{{y}}{\pi}×\frac{\pi}{{sin}\left(\pi.\frac{{y}}{\pi}\right)}\:=\frac{{y}}{{siny}}\:\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dx}}{\left(^{{y}} \sqrt{{x}^{\pi} }+\mathrm{1}\right)}{dy} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{y}}{{siny}}{dy}\:…{we}\:{can}\:{find}\:{a}\:{approximat}\:{value}\:{for}\:{this}\:{integral} \\ $$$$…{be}\:{continued}… \\ $$
Commented by mathmax by abdo last updated on 03/Feb/20

$${changement}\:{tan}\left(\frac{{y}}{\mathrm{2}}\right)={t}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{ydy}}{{siny}}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{arctan}\left({t}\right)}{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}×\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({t}\right){dt}\: \\ $$$${we}\:{have}\:{arctan}^{'} \left({t}\right)=\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} \:{t}^{\mathrm{2}{n}} \:\Rightarrow \\ $$$${arctan}\left({t}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}{t}^{\mathrm{2}{n}} \:+\:{c}\:\left({c}=\mathrm{0}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:{arctan}\left({t}\right){dt} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}{n}} \:{dt}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:={K}\left({constante}\:\:{of}\:{catalan}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{y}}{{siny}}{dy}\:=\mathrm{2}{K}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\left(^{{y}} \sqrt{{x}^{\pi} }+\mathrm{1}\right)}{dy} \\ $$
Commented by mathmax by abdo last updated on 03/Feb/20

$${K}\:\sim\:\mathrm{0},\mathrm{9159}… \\ $$
