Question Number 151220 by peter frank last updated on 19/Aug/21
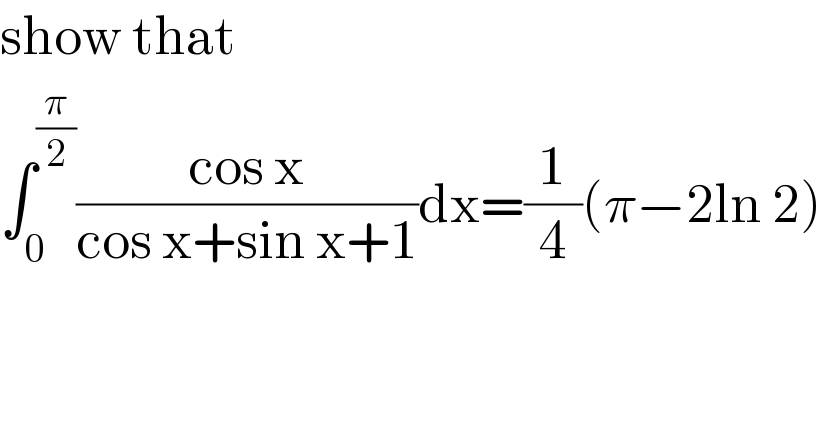
$$\mathrm{show}\:\mathrm{that}\: \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{cos}\:\mathrm{x}}{\mathrm{cos}\:\mathrm{x}+\mathrm{sin}\:\mathrm{x}+\mathrm{1}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{4}}\left(\pi−\mathrm{2ln}\:\mathrm{2}\right) \\ $$
Answered by ArielVyny last updated on 19/Aug/21

$${t}={tan}\left(\frac{{x}}{\mathrm{2}}\right)\rightarrow{dt}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }+\mathrm{1}}×\frac{\mathrm{2}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\left(\mathrm{1}−{t}^{\mathrm{2}} \right)+\left(\mathrm{2}{t}\right)+\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }×\frac{\mathrm{1}}{\mathrm{2}+\mathrm{2}{t}}{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{t}\right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}\:{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\frac{\pi}{\mathrm{4}}−\Sigma\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\frac{\pi}{\mathrm{4}}−\Sigma\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{2}}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right) \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{cosx}}{{cosx}+{sinx}+\mathrm{1}}=\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}+\right. \\ $$
Commented by peter frank last updated on 19/Aug/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Lordose last updated on 19/Aug/21
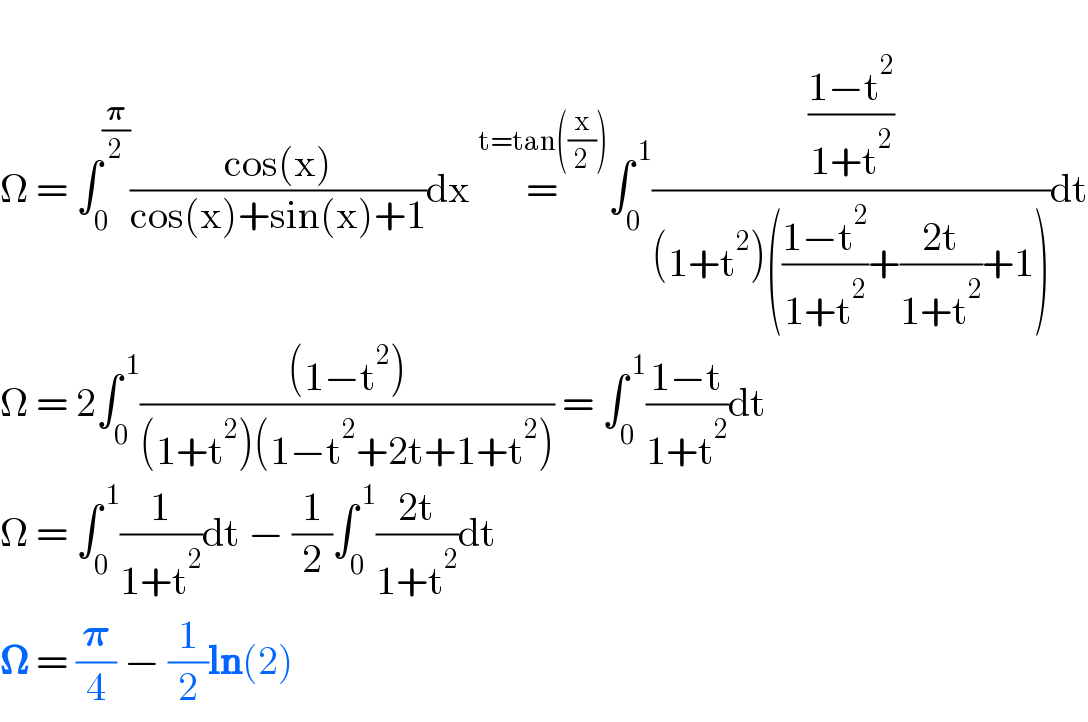
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{x}\right)+\mathrm{1}}\mathrm{dx}\:\overset{\mathrm{t}=\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\mathrm{1}\right)}\mathrm{dt} \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\boldsymbol{\Omega}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{4}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right) \\ $$
Commented by peter frank last updated on 19/Aug/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by Lordose last updated on 19/Aug/21
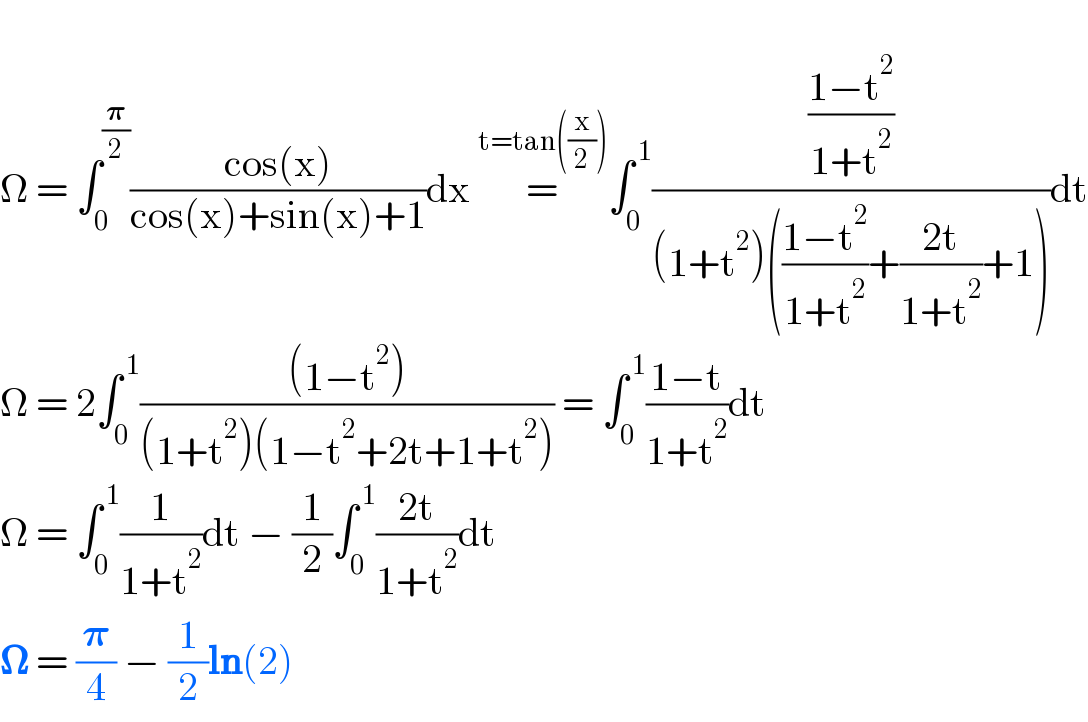
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \frac{\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{x}\right)+\mathrm{1}}\mathrm{dx}\:\overset{\mathrm{t}=\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }+\mathrm{1}\right)}\mathrm{dt} \\ $$$$\Omega\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−\mathrm{t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{2t}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\boldsymbol{\Omega}\:=\:\frac{\boldsymbol{\pi}}{\mathrm{4}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right) \\ $$
