Menu Close

Show-that-0-x-2-ln-x-x-4-x-2-1-dx-pi-2-12-

Tinku Tara 0 Comments
Pin




Question Number 130053 by Lordose last updated on 22/Jan/21
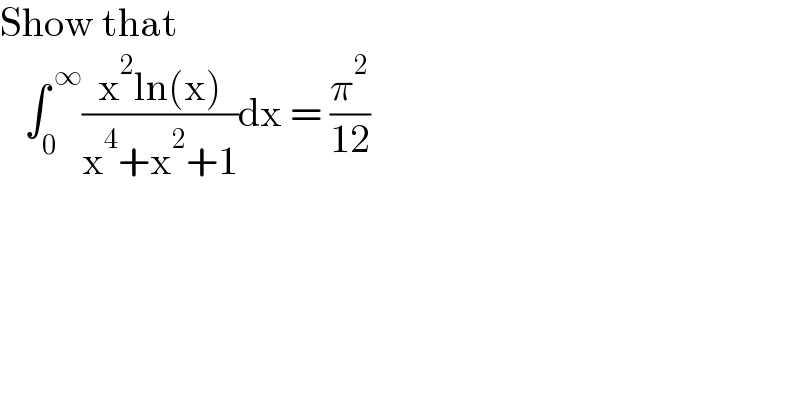
Show that ∫_0 ^( ∞) ((x^2 ln(x))/(x^4 +x^2 +1))dx = (π^2 /(12))
$$\mathrm{Show}\:\mathrm{that} \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
Answered by Ar Brandon last updated on 22/Jan/21
f(a)=∫_0 ^∞ ((x^2 ln(ax))/(x^4 +x^2 +1))dx f ′(a)=∫_0 ^∞ (x/(x^4 +x^2 +1))dx , x^2 =u =(1/2)∫_0 ^∞ (du/(u^2 +u+1))=(1/2)∫_0 ^∞ (du/((u+(1/2))^2 +(3/4))) =(1/( 2(√3)))[tan^(−1) (((2u+1)/( (√3))))]_0 ^∞ =(1/( 2(√3)))[(π/2)−(π/6)]=(π/( 6(√3))) f(a)=(π/(6(√3)))a+C...
$$\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{ax}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx} \\ $$$$\mathrm{f}\:'\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:,\:\mathrm{x}^{\mathrm{2}} =\mathrm{u} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{u}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{du}}{\left(\mathrm{u}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{3}}}\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2u}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{3}}}\left[\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{6}}\right]=\frac{\pi}{\:\mathrm{6}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\frac{\pi}{\mathrm{6}\sqrt{\mathrm{3}}}\mathrm{a}+\mathcal{C}… \\ $$
Answered by mathmax by abdo last updated on 22/Jan/21
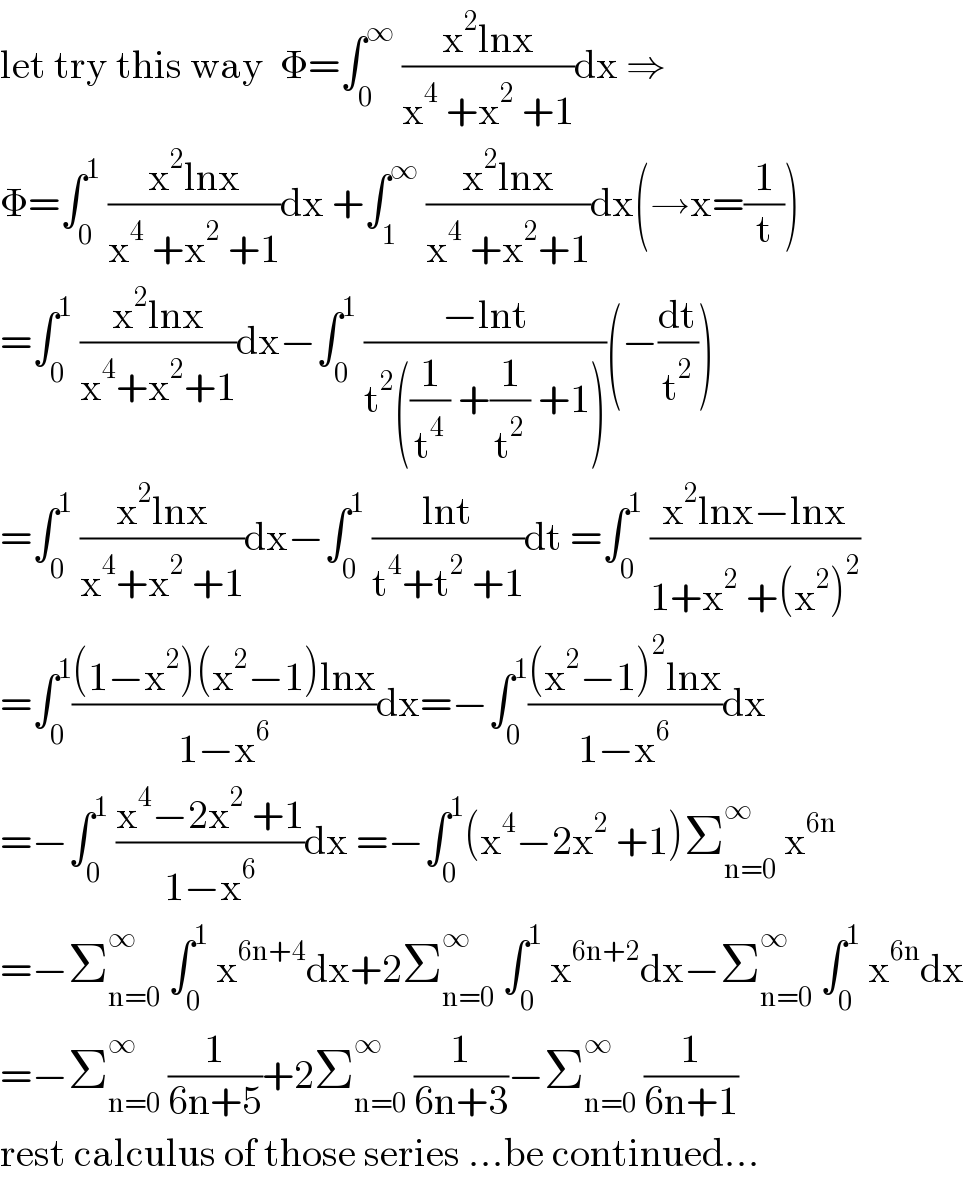
let try this way Φ=∫_0 ^∞ ((x^2 lnx)/(x^4 +x^2 +1))dx ⇒ Φ=∫_0 ^1 ((x^2 lnx)/(x^4 +x^2 +1))dx +∫_1 ^∞ ((x^2 lnx)/(x^4 +x^2 +1))dx(→x=(1/t)) =∫_0 ^1 ((x^2 lnx)/(x^4 +x^2 +1))dx−∫_0 ^1 ((−lnt)/(t^2 ((1/t^4 ) +(1/t^2 ) +1)))(−(dt/t^2 )) =∫_0 ^1 ((x^2 lnx)/(x^4 +x^2 +1))dx−∫_0 ^1 ((lnt)/(t^4 +t^2 +1))dt =∫_0 ^1 ((x^2 lnx−lnx)/(1+x^2 +(x^2 )^2 )) =∫_0 ^1 (((1−x^2 )(x^2 −1)lnx)/(1−x^6 ))dx=−∫_0 ^1 (((x^2 −1)^2 lnx)/(1−x^6 ))dx =−∫_0 ^1 ((x^4 −2x^2 +1)/(1−x^6 ))dx =−∫_0 ^1 (x^4 −2x^2 +1)Σ_(n=0) ^∞ x^(6n) =−Σ_(n=0) ^∞ ∫_0 ^1 x^(6n+4) dx+2Σ_(n=0) ^∞ ∫_0 ^1 x^(6n+2) dx−Σ_(n=0) ^∞ ∫_0 ^1 x^(6n) dx =−Σ_(n=0) ^∞ (1/(6n+5))+2Σ_(n=0) ^∞ (1/(6n+3))−Σ_(n=0) ^∞ (1/(6n+1)) rest calculus of those series ...be continued...
$$\mathrm{let}\:\mathrm{try}\:\mathrm{this}\:\mathrm{way}\:\:\Phi=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:\Rightarrow \\ $$$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} \:+\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\left(\rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{lnt}}{\mathrm{t}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{4}} }\:+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\:+\mathrm{1}\right)}\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnt}}{\mathrm{t}^{\mathrm{4}} +\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}}\mathrm{dt}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2}} \mathrm{lnx}−\mathrm{lnx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} \:+\left(\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{lnx}}{\mathrm{1}−\mathrm{x}^{\mathrm{6}} }\mathrm{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \mathrm{lnx}}{\mathrm{1}−\mathrm{x}^{\mathrm{6}} }\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{1}−\mathrm{x}^{\mathrm{6}} }\mathrm{dx}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{4}} −\mathrm{2x}^{\mathrm{2}} \:+\mathrm{1}\right)\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{6n}} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{6n}+\mathrm{4}} \mathrm{dx}+\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{6n}+\mathrm{2}} \mathrm{dx}−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{6n}} \mathrm{dx} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{6n}+\mathrm{5}}+\mathrm{2}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{6n}+\mathrm{3}}−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{6n}+\mathrm{1}} \\ $$$$\mathrm{rest}\:\mathrm{calculus}\:\mathrm{of}\:\mathrm{those}\:\mathrm{series}\:…\mathrm{be}\:\mathrm{continued}… \\ $$
Answered by mnjuly1970 last updated on 22/Jan/21
φ=∫_(0 ) ^( 1) ((x^2 ln(x))/(1+x^2 +x^4 ))dx+[∫_1 ^( ∞) ((x^2 ln(x))/(1+x^2 +x^4 ))dx =Φ] Φ=∫_0 ^( 1) ((−ln(x) )/(1+x^2 +x^4 ))dx ∅=∫_0 ^( 1) (((x^2 −1)ln(x))/(1+x^2 +x^4 ))dx=∫_0 ^( 1) ((−(x^2 −1)^2 ln(x))/(1−x^6 ))dx =−∫_0 ^( 1) (((x^4 −2x^2 +1)ln(x))/(1−x^6 )) =^(x^6 =t) −(1/6)∫_0 ^( 1) (((t^(2/3) −2t^(1/3) +1)t^((−5)/6) ln(t))/(1−t))dt =((−1)/(36))∫_0 ^( 1() ((t^((−1)/6) −2t^((−1)/2) +t^((−5)/6) )ln(t))/(1−t))dt f(a)=∫_0 ^( 1) ((t^(a−(1/6)) −2t^(a−(1/2)) +t^(a−(5/6)) )/(1−t))dt φ=((−1)/(36))f ′(0) f(a)=∫_0 ^( 1) ((t^(a−(1/6)) −1+1−t^(a−(1/2)) −1+t^(a−(5/6)) −t^(a−(1/2)) +1)/(1−t))dt =−ψ(a+(5/6))+2ψ(a+(1/2))−ψ(a+(1/6)) =−ψ(a+(5/6))−ψ(a+(1/6))+2ψ(a+(1/2)) f ′(a)=−ψ′(a+(5/6))−ψ′(a+(1/6))+2ψ′(a+(1/2)) f ′(0)=−ψ′((5/6))−ψ′((1/6))+2ψ′((1/2)) =−(π^2 /(sin^2 ((π/6))))+2 (π^2 /2)=−3π^2 φ=(π^2 /(12)) .....✓✓ m.n.july.1970
$$\:\:\phi=\int_{\mathrm{0}\:} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{2}} {ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}+\left[\int_{\mathrm{1}} ^{\:\infty} \frac{{x}^{\mathrm{2}} {ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}\:=\Phi\right] \\ $$$$\Phi=\int_{\mathrm{0}} ^{\:\:\mathrm{1}} \frac{−{ln}\left({x}\right)\:\:}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx} \\ $$$$\emptyset=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({x}^{\mathrm{2}} −\mathrm{1}\right){ln}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{4}} }{dx}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{−\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} {ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{6}} }{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{1}\right){ln}\left({x}\right)}{\mathrm{1}−{x}^{\mathrm{6}} } \\ $$$$\overset{{x}^{\mathrm{6}} ={t}} {=}−\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({t}^{\frac{\mathrm{2}}{\mathrm{3}}} −\mathrm{2}{t}^{\frac{\mathrm{1}}{\mathrm{3}}} +\mathrm{1}\right){t}^{\frac{−\mathrm{5}}{\mathrm{6}}} {ln}\left({t}\right)}{\mathrm{1}−{t}}{dt} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\:\mathrm{1}\left(\right.} \frac{\left.{t}^{\frac{−\mathrm{1}}{\mathrm{6}}} −\mathrm{2}{t}^{\frac{−\mathrm{1}}{\mathrm{2}}} +{t}^{\frac{−\mathrm{5}}{\mathrm{6}}} \right){ln}\left({t}\right)}{\mathrm{1}−{t}}{dt}\: \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}^{{a}−\frac{\mathrm{1}}{\mathrm{6}}} −\mathrm{2}{t}^{{a}−\frac{\mathrm{1}}{\mathrm{2}}} +{t}^{{a}−\frac{\mathrm{5}}{\mathrm{6}}} }{\mathrm{1}−{t}}{dt} \\ $$$$\:\phi=\frac{−\mathrm{1}}{\mathrm{36}}{f}\:'\left(\mathrm{0}\right) \\ $$$$\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{t}^{{a}−\frac{\mathrm{1}}{\mathrm{6}}} −\mathrm{1}+\mathrm{1}−{t}^{{a}−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{1}+{t}^{{a}−\frac{\mathrm{5}}{\mathrm{6}}} −{t}^{{a}−\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}}{\mathrm{1}−{t}}{dt} \\ $$$$=−\psi\left({a}+\frac{\mathrm{5}}{\mathrm{6}}\right)+\mathrm{2}\psi\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left({a}+\frac{\mathrm{1}}{\mathrm{6}}\right) \\ $$$$=−\psi\left({a}+\frac{\mathrm{5}}{\mathrm{6}}\right)−\psi\left({a}+\frac{\mathrm{1}}{\mathrm{6}}\right)+\mathrm{2}\psi\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${f}\:'\left({a}\right)=−\psi'\left({a}+\frac{\mathrm{5}}{\mathrm{6}}\right)−\psi'\left({a}+\frac{\mathrm{1}}{\mathrm{6}}\right)+\mathrm{2}\psi'\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${f}\:'\left(\mathrm{0}\right)=−\psi'\left(\frac{\mathrm{5}}{\mathrm{6}}\right)−\psi'\left(\frac{\mathrm{1}}{\mathrm{6}}\right)+\mathrm{2}\psi'\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:=−\frac{\pi^{\mathrm{2}} }{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{6}}\right)}+\mathrm{2}\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}}=−\mathrm{3}\pi^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\phi=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:…..\checkmark\checkmark\:\:{m}.{n}.{july}.\mathrm{1970} \\ $$$$ \\ $$
Answered by Lordose last updated on 22/Jan/21
𝛀 = lim_(𝛆→0) ∫_𝛆 ^( ∞) ((x^2 ln(x))/(x^4 +x^2 +1))dx = (∫_1 ^( ∞) ((x^2 ln(x))/(x^4 +x^2 +1))dx + ∫_0 ^( 1) ((x^2 ln(x))/(x^4 +x^2 +1))dx) Ω = Φ + Ψ Ψ = ∫_0 ^( ∞) ((x^2 ln(x))/(x^4 +x^2 +1))dx =^(u=(1/x)) ∫_1 ^( 0) −((−((1/u^2 ))ln(u))/(u^2 ((1/u^4 )+(1/u^2 )+1)))du = −∫_0 ^( 1) ((ln(u))/(u^4 +u^2 +1))du Ω = ∫_0 ^( 1) ((x^2 ln(x)−ln(x))/(x^4 +x^2 +1))dx = ∫_0 ^( 1) (((1−x^2 )(x^2 −1)ln(x))/(1−x^6 ))dx = −∫_0 ^( 1) (((x^2 −1)^2 ln(x))/(1−x^6 ))dx Ω =^(t=x^6 ) −∫_0 ^( 1) (((1/6)(t^(1/3) −1)^2 ln(t))/(1−t)) ((t^(−(5/6)) dt)/6) = −(1/(36))∫_0 ^( 1) (((t^((4/6)−(5/6)) −2t^((2/6)−(5/6)) +t^(−(5/6)) )ln(t))/(1−t))dt Ω(n) = ∫_0 ^( 1) (((t^(−(1/6)+n) −2t^(−(1/2)+n) +t^(−(5/6)+n) ))/(1−t))dt Ω = −(1/(36))Ω^′ (0) Ω(n) = ∫_0 ^( 1) ((t^(n−(1/6)) −2t^(n−(1/2)) +t^(n−(5/6)) )/(1−t))dt Ω(n) = −𝛙^((0)) (n+(1/6)) − 𝛙^((0)) (n+(5/6)) + 2𝛙^((0)) (n+(1/2)) Ω′(n) = −𝛙^((0)^′ ) (n+(1/6)) − 𝛙^((0)^′ ) (n+(5/6)) + 2𝛙^((0)′) (n+(1/2)) Ω′(0) = −(𝛙^((0)′) ((1/6)) + 𝛙^((0)′) ((5/6))) + 2𝛙^((0)′) ((1/2)) Ω′(0) = −(π^2 csc^2 ((π/6)))+2 (π^2 /2)=−3π^2 Ω = −(1/(36))Ω′(0) = (1/(36))∙3π^2 = (π^2 /(12)) ★L𝛗rD ∅sE
$$ \\ $$$$\boldsymbol{\Omega}\:=\:\underset{\boldsymbol{\epsilon}\rightarrow\mathrm{0}} {\mathrm{lim}}\int_{\boldsymbol{\epsilon}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\:\left(\int_{\mathrm{1}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\right) \\ $$$$\Omega\:=\:\Phi\:+\:\Psi \\ $$$$\Psi\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:\overset{\mathrm{u}=\frac{\mathrm{1}}{\mathrm{x}}} {=}\int_{\mathrm{1}} ^{\:\mathrm{0}} \:−\frac{−\left(\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)\mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{u}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }+\mathrm{1}\right)}\mathrm{du}\:=\:−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{u}^{\mathrm{4}} +\mathrm{u}^{\mathrm{2}} +\mathrm{1}}\mathrm{du} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)−\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}^{\mathrm{6}} }\mathrm{dx}\:=\:−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}^{\mathrm{6}} }\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{t}=\mathrm{x}^{\mathrm{6}} } {=}−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\frac{\mathrm{1}}{\mathrm{6}}\left(\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} −\mathrm{1}\right)^{\mathrm{2}} \mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}−\mathrm{t}}\:\frac{\mathrm{t}^{−\frac{\mathrm{5}}{\mathrm{6}}} \mathrm{dt}}{\mathrm{6}}\:=\:−\frac{\mathrm{1}}{\mathrm{36}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{t}^{\frac{\mathrm{4}}{\mathrm{6}}−\frac{\mathrm{5}}{\mathrm{6}}} −\mathrm{2t}^{\frac{\mathrm{2}}{\mathrm{6}}−\frac{\mathrm{5}}{\mathrm{6}}} +\mathrm{t}^{−\frac{\mathrm{5}}{\mathrm{6}}} \right)\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}−\mathrm{t}}\mathrm{dt} \\ $$$$\Omega\left(\mathrm{n}\right)\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{6}}+\mathrm{n}} −\mathrm{2t}^{−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{n}} +\mathrm{t}^{−\frac{\mathrm{5}}{\mathrm{6}}+\mathrm{n}} \right)}{\mathrm{1}−\mathrm{t}}\mathrm{dt} \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{36}}\Omega^{'} \left(\mathrm{0}\right) \\ $$$$\Omega\left(\mathrm{n}\right)\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{t}^{\mathrm{n}−\frac{\mathrm{1}}{\mathrm{6}}} −\mathrm{2t}^{\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{t}^{\mathrm{n}−\frac{\mathrm{5}}{\mathrm{6}}} }{\mathrm{1}−\mathrm{t}}{dt} \\ $$$$\Omega\left(\mathrm{n}\right)\:=\:−\boldsymbol{\psi}^{\left(\mathrm{0}\right)} \left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{6}}\right)\:−\:\boldsymbol{\psi}^{\left(\mathrm{0}\right)} \left(\mathrm{n}+\frac{\mathrm{5}}{\mathrm{6}}\right)\:+\:\mathrm{2}\boldsymbol{\psi}^{\left(\mathrm{0}\right)} \left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Omega'\left(\mathrm{n}\right)\:=\:−\boldsymbol{\psi}^{\left(\mathrm{0}\right)^{'} } \left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{6}}\right)\:−\:\boldsymbol{\psi}^{\left(\mathrm{0}\right)^{'} } \left(\mathrm{n}+\frac{\mathrm{5}}{\mathrm{6}}\right)\:+\:\mathrm{2}\boldsymbol{\psi}^{\left(\mathrm{0}\right)'} \left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Omega'\left(\mathrm{0}\right)\:=\:−\left(\boldsymbol{\psi}^{\left(\mathrm{0}\right)'} \left(\frac{\mathrm{1}}{\mathrm{6}}\right)\:+\:\boldsymbol{\psi}^{\left(\mathrm{0}\right)'} \left(\frac{\mathrm{5}}{\mathrm{6}}\right)\right)\:+\:\mathrm{2}\boldsymbol{\psi}^{\left(\mathrm{0}\right)'} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Omega'\left(\mathrm{0}\right)\:=\:−\left(\pi^{\mathrm{2}} \mathrm{csc}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{6}}\right)\right)+\mathrm{2}\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}}=−\mathrm{3}\pi^{\mathrm{2}} \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{36}}\Omega'\left(\mathrm{0}\right)\:=\:\frac{\mathrm{1}}{\mathrm{36}}\centerdot\mathrm{3}\pi^{\mathrm{2}} \:=\:\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\bigstar\boldsymbol{\mathrm{L}\phi\mathrm{rD}}\:\boldsymbol{\varnothing\mathrm{sE}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *