Menu Close

Show-that-0-x-3-e-x-1-dx-pi-4-15-

Tinku Tara 0 Comments
Pin




Question Number 78797 by TawaTawa last updated on 20/Jan/20
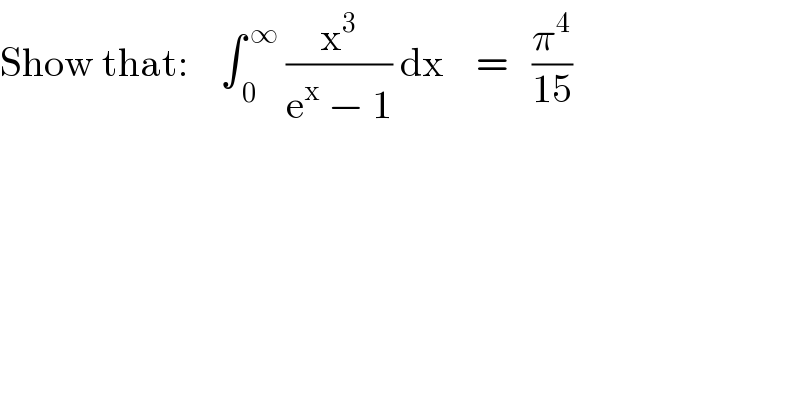
Show that: ∫_( 0) ^( ∞) (x^3 /(e^x − 1)) dx = (π^4 /(15))
$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\int_{\:\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{e}^{\mathrm{x}} \:−\:\mathrm{1}}\:\mathrm{dx}\:\:\:\:=\:\:\:\frac{\pi^{\mathrm{4}} }{\mathrm{15}} \\ $$
Answered by mind is power last updated on 20/Jan/20
=∫_0 ^(+∞) ((x^3 e^(−x) )/(1−e^(−x) ))dx (1/(1−e^(−x) ))=Σ_(k≥0) e^(−kx) ⇒=∫_0 ^(+∞) x^3 e^(−x) Σ_(k≥0) e^(−kx) dx =∫_0 ^(+∞) x^3 Σ_(k≥0) e^(−(1+k)x) =Σ∫_0 ^(+∞) x^3 e^(−(1+k)x) dx u=(1+k)x⇒dx=(du/(1+k)) =Σ_(k≥0) ∫_0 ^(+∞) (u^3 /((1+k)^4 ))e^(−u) du one of definition of Γ(x)=∫_0 ^(+∞) t^(x−1) e^(−t) dt =Σ_(k≥0) ((Γ(4))/((1+k)^4 ))=Σ_(k≥0) (6/((1+k)^4 ))=Σ_(n≥1) (6/n^4 )=6ζ(4)=6.(π^4 /(90))=(π^4 /(15)) ∫_0 ^(+∞) (x^3 /(e^x −1))dx=(π^4 /(15)) mor generaly if a>0 ∫_0 ^(+∞) (x^a /(e^x −1))dx=Γ(a+1).ζ(a+1)
$$=\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{x}^{\mathrm{3}} \mathrm{e}^{−\mathrm{x}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{x}} }\mathrm{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\mathrm{e}^{−\mathrm{x}} }=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\mathrm{e}^{−\mathrm{kx}} \\ $$$$\Rightarrow=\int_{\mathrm{0}} ^{+\infty} \mathrm{x}^{\mathrm{3}} \mathrm{e}^{−\mathrm{x}} \underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\mathrm{e}^{−\mathrm{kx}} \mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \mathrm{x}^{\mathrm{3}} \underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\mathrm{e}^{−\left(\mathrm{1}+\mathrm{k}\right)\mathrm{x}} \\ $$$$=\Sigma\int_{\mathrm{0}} ^{+\infty} \mathrm{x}^{\mathrm{3}} \mathrm{e}^{−\left(\mathrm{1}+\mathrm{k}\right)\mathrm{x}} \mathrm{dx} \\ $$$$\mathrm{u}=\left(\mathrm{1}+\mathrm{k}\right)\mathrm{x}\Rightarrow\mathrm{dx}=\frac{\mathrm{du}}{\mathrm{1}+\mathrm{k}} \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{u}^{\mathrm{3}} }{\left(\mathrm{1}+\mathrm{k}\right)^{\mathrm{4}} }\mathrm{e}^{−\mathrm{u}} \mathrm{du} \\ $$$$\mathrm{one}\:\mathrm{of}\:\mathrm{definition}\:\mathrm{of}\:\:\Gamma\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{+\infty} \mathrm{t}^{\mathrm{x}−\mathrm{1}} \mathrm{e}^{−\mathrm{t}} \mathrm{dt} \\ $$$$=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\Gamma\left(\mathrm{4}\right)}{\left(\mathrm{1}+\mathrm{k}\right)^{\mathrm{4}} }=\underset{\mathrm{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{6}}{\left(\mathrm{1}+\mathrm{k}\right)^{\mathrm{4}} }=\underset{\mathrm{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{6}}{\mathrm{n}^{\mathrm{4}} }=\mathrm{6}\zeta\left(\mathrm{4}\right)=\mathrm{6}.\frac{\pi^{\mathrm{4}} }{\mathrm{90}}=\frac{\pi^{\mathrm{4}} }{\mathrm{15}} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\mathrm{dx}=\frac{\pi^{\mathrm{4}} }{\mathrm{15}} \\ $$$$\mathrm{mor}\:\mathrm{generaly}\:\mathrm{if}\:\mathrm{a}>\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{x}^{\mathrm{a}} }{\mathrm{e}^{\mathrm{x}} −\mathrm{1}}\mathrm{dx}=\Gamma\left(\mathrm{a}+\mathrm{1}\right).\zeta\left(\mathrm{a}+\mathrm{1}\right) \\ $$$$ \\ $$
Commented by TawaTawa last updated on 20/Jan/20
Wow, God bless you sir.
$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by mind is power last updated on 20/Jan/20
thanx sir ,most Welcom
$$\mathrm{thanx}\:\mathrm{sir}\:,\mathrm{most}\:\mathrm{Welcom} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *