Menu Close

show-that-0-x-pi-5-1-1-x-2pi-dx-

Tinku Tara 0 Comments
Pin




Question Number 80924 by M±th+et£s last updated on 08/Feb/20
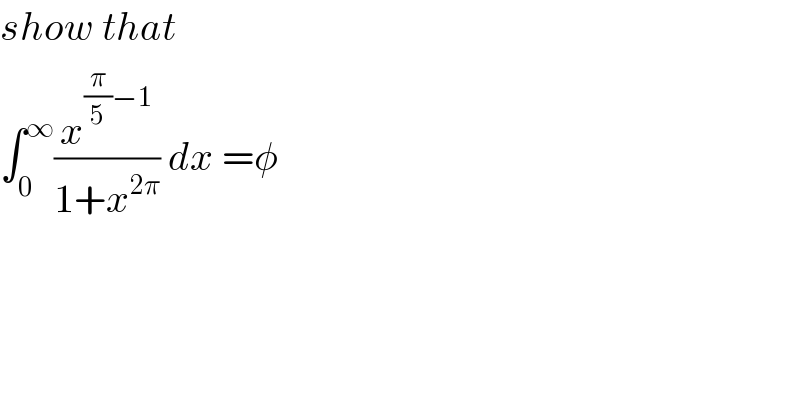
show that ∫_0 ^∞ (x^((π/5)−1) /(1+x^(2π) )) dx =φ
$${show}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\frac{\pi}{\mathrm{5}}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}\pi} }\:{dx}\:=\phi\: \\ $$
Commented by abdomathmax last updated on 09/Feb/20
changement x^(2π) =t give x=t^(1/(2π)) ⇒ ∫_0 ^∞ (x^((π/5)−1) /(1+x^(2π) ))dx =∫_0 ^∞ (((t^(1/(2π)) )^((π/5)−1) )/(1+t))×(1/(2π))t^((1/(2π))−1) dt =(1/(2π))∫_0 ^∞ (t^((1/(10))−(1/(2π))+(1/(2π))−1) /(1+t))dt =(1/(2π))∫_0 ^∞ (t^((1/(10))−1) /(1+t))dt =(1/(2π))×(π/(sin((π/(10))))) =(1/(2sin((π/(10))))) we know cos((π/5))=((1+(√5))/4) sin^2 ((π/(10)))=((1−cos((π/5)))/2)=((1−((1+(√5))/4))/2) =((3−(√5))/8) ⇒sin((π/(10)))=(√((3−(√5))/8)) ((((√5)−1)/4))^2 =((6−2(√5))/(16)) =((3−(√5))/8) ⇒sin((π/(10)))=(((√5)−1)/4) ⇒ I=(1/(((√5)−1)/2)) =ϕ
$${changement}\:{x}^{\mathrm{2}\pi} ={t}\:{give}\:{x}={t}^{\frac{\mathrm{1}}{\mathrm{2}\pi}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\frac{\pi}{\mathrm{5}}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}\pi} }{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\left({t}^{\frac{\mathrm{1}}{\mathrm{2}\pi}} \right)^{\frac{\pi}{\mathrm{5}}−\mathrm{1}} }{\mathrm{1}+{t}}×\frac{\mathrm{1}}{\mathrm{2}\pi}{t}^{\frac{\mathrm{1}}{\mathrm{2}\pi}−\mathrm{1}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{10}}−\frac{\mathrm{1}}{\mathrm{2}\pi}+\frac{\mathrm{1}}{\mathrm{2}\pi}−\mathrm{1}} }{\mathrm{1}+{t}}{dt}\:=\frac{\mathrm{1}}{\mathrm{2}\pi}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{\frac{\mathrm{1}}{\mathrm{10}}−\mathrm{1}} }{\mathrm{1}+{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}×\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{10}}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$${we}\:{know}\:{cos}\left(\frac{\pi}{\mathrm{5}}\right)=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$${sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{10}}\right)=\frac{\mathrm{1}−{cos}\left(\frac{\pi}{\mathrm{5}}\right)}{\mathrm{2}}=\frac{\mathrm{1}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{8}}\:\Rightarrow{sin}\left(\frac{\pi}{\mathrm{10}}\right)=\sqrt{\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{8}}} \\ $$$$\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} =\frac{\mathrm{6}−\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{16}}\:=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{8}}\:\Rightarrow{sin}\left(\frac{\pi}{\mathrm{10}}\right)=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${I}=\frac{\mathrm{1}}{\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}}}\:=\varphi \\ $$
Commented by M±th+et£s last updated on 09/Feb/20
god bless you sir
$${god}\:{bless}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 10/Feb/20
you are welvome sir.
$${you}\:{are}\:{welvome}\:{sir}. \\ $$
Answered by mind is power last updated on 09/Feb/20
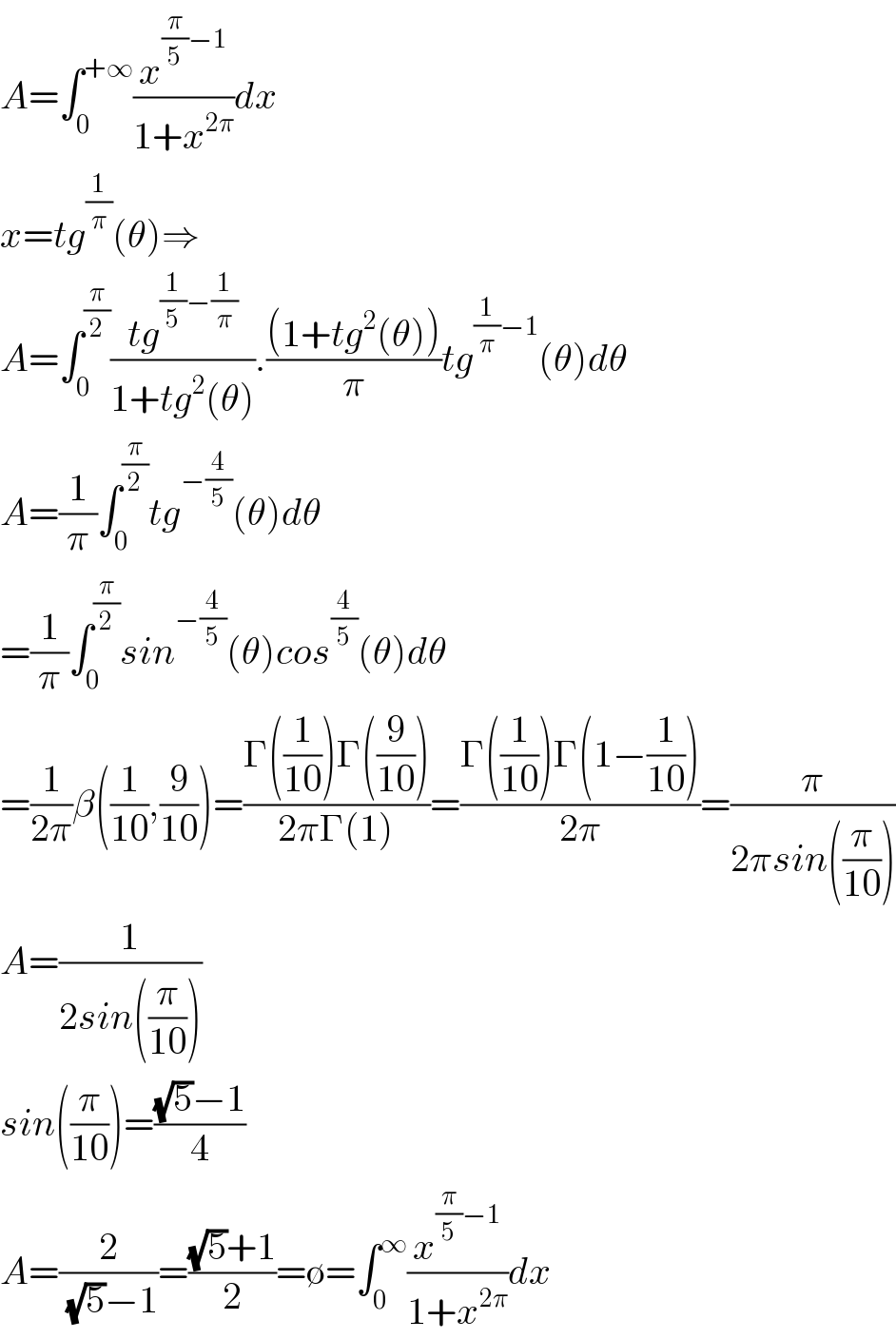
A=∫_0 ^(+∞) (x^((π/5)−1) /(1+x^(2π) ))dx x=tg^(1/π) (θ)⇒ A=∫_0 ^(π/2) ((tg^((1/5)−(1/π)) )/(1+tg^2 (θ))).(((1+tg^2 (θ)))/π)tg^((1/π)−1) (θ)dθ A=(1/π)∫_0 ^(π/2) tg^(−(4/5)) (θ)dθ =(1/π)∫_0 ^(π/2) sin^(−(4/5)) (θ)cos^(4/5) (θ)dθ =(1/(2π))β((1/(10)),(9/(10)))=((Γ((1/(10)))Γ((9/(10))))/(2πΓ(1)))=((Γ((1/(10)))Γ(1−(1/(10))))/(2π))=(π/(2πsin((π/(10))))) A=(1/(2sin((π/(10))))) sin((π/(10)))=(((√5)−1)/4) A=(2/( (√5)−1))=(((√5)+1)/2)=∅=∫_0 ^∞ (x^((π/5)−1) /(1+x^(2π) ))dx
$${A}=\int_{\mathrm{0}} ^{+\infty} \frac{{x}^{\frac{\pi}{\mathrm{5}}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}\pi} }{dx} \\ $$$${x}={tg}^{\frac{\mathrm{1}}{\pi}} \left(\theta\right)\Rightarrow \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{tg}^{\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\pi}} }{\mathrm{1}+{tg}^{\mathrm{2}} \left(\theta\right)}.\frac{\left(\mathrm{1}+{tg}^{\mathrm{2}} \left(\theta\right)\right)}{\pi}{tg}^{\frac{\mathrm{1}}{\pi}−\mathrm{1}} \left(\theta\right){d}\theta \\ $$$${A}=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {tg}^{−\frac{\mathrm{4}}{\mathrm{5}}} \left(\theta\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {sin}^{−\frac{\mathrm{4}}{\mathrm{5}}} \left(\theta\right){cos}^{\frac{\mathrm{4}}{\mathrm{5}}} \left(\theta\right){d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\beta\left(\frac{\mathrm{1}}{\mathrm{10}},\frac{\mathrm{9}}{\mathrm{10}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{10}}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{10}}\right)}{\mathrm{2}\pi\Gamma\left(\mathrm{1}\right)}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{10}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}\right)}{\mathrm{2}\pi}=\frac{\pi}{\mathrm{2}\pi{sin}\left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}{sin}\left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$${sin}\left(\frac{\pi}{\mathrm{10}}\right)=\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{4}} \\ $$$${A}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}−\mathrm{1}}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}=\emptyset=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\frac{\pi}{\mathrm{5}}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}\pi} }{dx} \\ $$
Commented by M±th+et£s last updated on 09/Feb/20
great sir thank you
$${great}\:{sir}\:{thank}\:{you} \\ $$
Commented by mind is power last updated on 09/Feb/20
Withe pleasur have you somm Quation about hypergeometric Function ?
$${Withe}\:{pleasur}\:\:{have}\:{you}\:{somm}\:{Quation} \\ $$$${about}\:{hypergeometric}\:{Function}\:? \\ $$
Commented by M±th+et£s last updated on 09/Feb/20
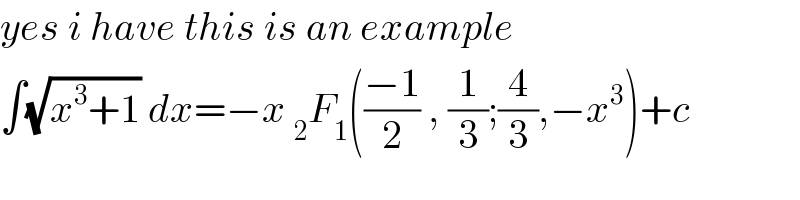
yes i have this is an example ∫(√(x^3 +1)) dx=−x _2 F_1 (((−1)/2) , (1/3);(4/3),−x^3 )+c
$${yes}\:{i}\:{have}\:{this}\:{is}\:{an}\:{example} \\ $$$$\int\sqrt{{x}^{\mathrm{3}} +\mathrm{1}}\:{dx}=−{x}\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{−\mathrm{1}}{\mathrm{2}}\:,\:\frac{\mathrm{1}}{\mathrm{3}};\frac{\mathrm{4}}{\mathrm{3}},−{x}^{\mathrm{3}} \right)+{c} \\ $$
Commented by M±th+et£s last updated on 09/Feb/20
i need some time to post all of my equations
$${i}\:{need}\:{some}\:{time}\:{to}\:{post}\:{all}\:{of}\:{my}\:{equations} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *