Question Number 120711 by TITA last updated on 02/Nov/20
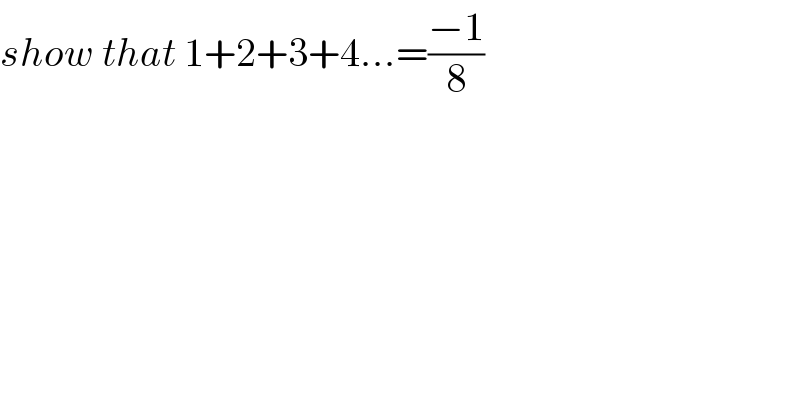
$${show}\:{that}\:\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}…=\frac{−\mathrm{1}}{\mathrm{8}} \\ $$
Answered by Dwaipayan Shikari last updated on 02/Nov/20
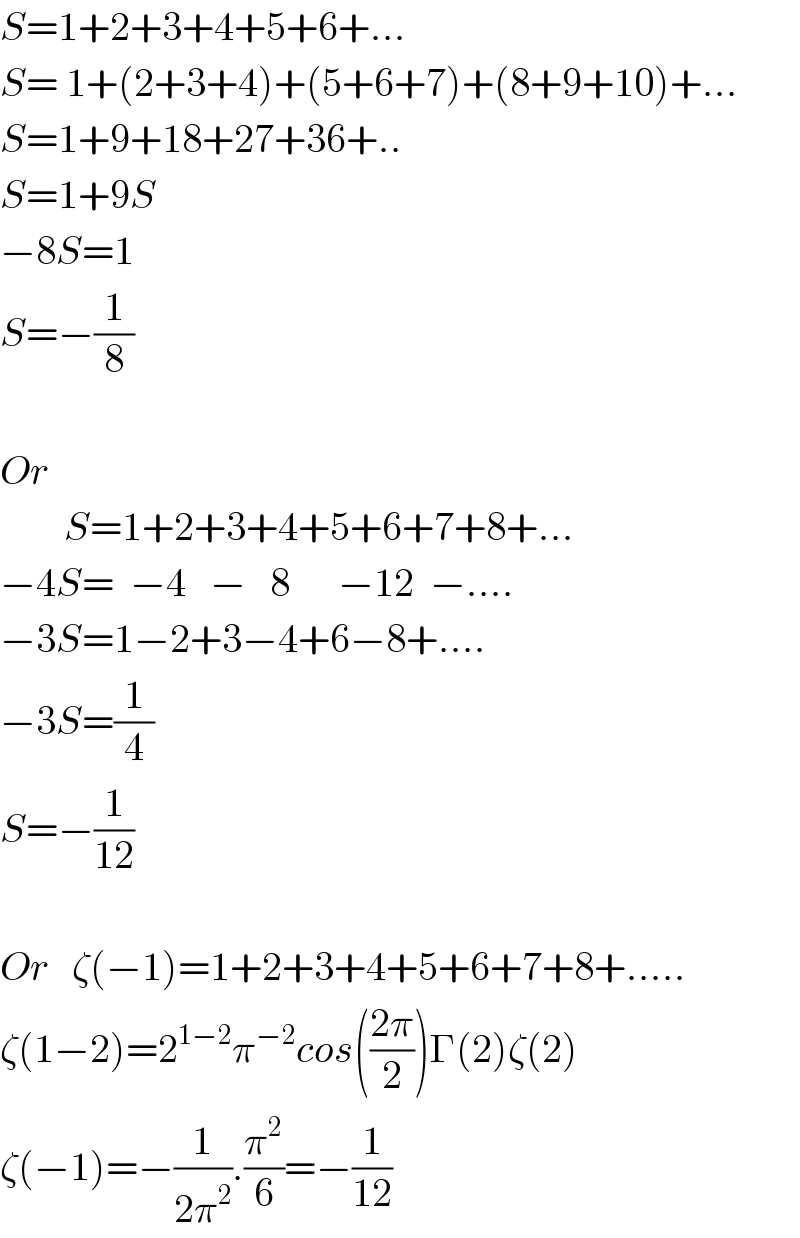
$${S}=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+… \\ $$$${S}=\:\mathrm{1}+\left(\mathrm{2}+\mathrm{3}+\mathrm{4}\right)+\left(\mathrm{5}+\mathrm{6}+\mathrm{7}\right)+\left(\mathrm{8}+\mathrm{9}+\mathrm{10}\right)+… \\ $$$${S}=\mathrm{1}+\mathrm{9}+\mathrm{18}+\mathrm{27}+\mathrm{36}+.. \\ $$$${S}=\mathrm{1}+\mathrm{9}{S} \\ $$$$−\mathrm{8}{S}=\mathrm{1} \\ $$$${S}=−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$ \\ $$$${Or} \\ $$$$\:\:\:\:\:\:\:\:{S}=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+… \\ $$$$−\mathrm{4}{S}=\:\:−\mathrm{4}\:\:\:−\:\:\:\mathrm{8}\:\:\:\:\:\:−\mathrm{12}\:\:−…. \\ $$$$−\mathrm{3}{S}=\mathrm{1}−\mathrm{2}+\mathrm{3}−\mathrm{4}+\mathrm{6}−\mathrm{8}+…. \\ $$$$−\mathrm{3}{S}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${S}=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$ \\ $$$${Or}\:\:\:\zeta\left(−\mathrm{1}\right)=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+….. \\ $$$$\zeta\left(\mathrm{1}−\mathrm{2}\right)=\mathrm{2}^{\mathrm{1}−\mathrm{2}} \pi^{−\mathrm{2}} {cos}\left(\frac{\mathrm{2}\pi}{\mathrm{2}}\right)\Gamma\left(\mathrm{2}\right)\zeta\left(\mathrm{2}\right) \\ $$$$\zeta\left(−\mathrm{1}\right)=−\frac{\mathrm{1}}{\mathrm{2}\pi^{\mathrm{2}} }.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$
Commented by Dwaipayan Shikari last updated on 02/Nov/20
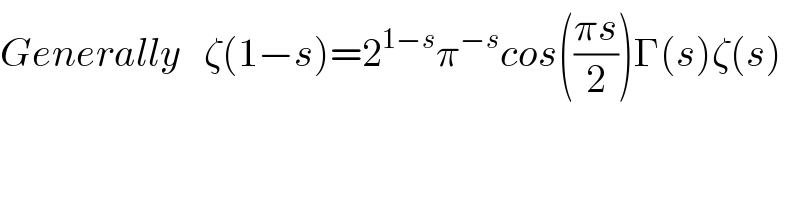
$${Generally}\:\:\:\zeta\left(\mathrm{1}−{s}\right)=\mathrm{2}^{\mathrm{1}−{s}} \pi^{−{s}} {cos}\left(\frac{\pi{s}}{\mathrm{2}}\right)\Gamma\left({s}\right)\zeta\left({s}\right) \\ $$
Answered by Rohit143Jo last updated on 02/Nov/20
![ans:- Let, 1+2+3+4+5+6+7+8+9+10+............=S ⇒1+9+18+27+36...........=S [∵2+3+4=9; 5+6+7=18 .....] ⇒1+9(1+2+3+4+.........)=S ⇒1+9S=S ⇒−8S=1 ⇒S=(−1/8)](https://www.tinkutara.com/question/Q120714.png)
$${ans}:-\:\:{Let},\:\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+\mathrm{9}+\mathrm{10}+…………={S} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{1}+\mathrm{9}+\mathrm{18}+\mathrm{27}+\mathrm{36}………..={S}\:\:\left[\because\mathrm{2}+\mathrm{3}+\mathrm{4}=\mathrm{9};\:\mathrm{5}+\mathrm{6}+\mathrm{7}=\mathrm{18}\:…..\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{1}+\mathrm{9}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+………\right)={S} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{1}+\mathrm{9}{S}={S} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow−\mathrm{8}{S}=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{S}=\left(−\mathrm{1}/\mathrm{8}\right) \\ $$
Commented by TITA last updated on 02/Nov/20

$${thanks} \\ $$
Answered by Rohit143Jo last updated on 02/Nov/20
![ans:- Let, 1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+.........=S ⇒1+2+25+50+75+........=S [∵3+4+5+6+7=25; 8+9+10+11+12=50 ...........] ⇒3+25(1+2+3+4+......)=S ⇒3+25S=S ⇒−24S=3 ⇒S=(−3/24) ⇒S=(−1/8)](https://www.tinkutara.com/question/Q120716.png)
$${ans}:-\:\:{Let},\:\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+\mathrm{9}+\mathrm{10}+\mathrm{11}+\mathrm{12}+\mathrm{13}+\mathrm{14}+\mathrm{15}+\mathrm{16}+\mathrm{17}+………={S} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{1}+\mathrm{2}+\mathrm{25}+\mathrm{50}+\mathrm{75}+……..={S}\:\:\left[\because\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}=\mathrm{25};\:\mathrm{8}+\mathrm{9}+\mathrm{10}+\mathrm{11}+\mathrm{12}=\mathrm{50}\:………..\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{3}+\mathrm{25}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+……\right)={S} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\mathrm{3}+\mathrm{25}{S}={S} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow−\mathrm{24}{S}=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{S}=\left(−\mathrm{3}/\mathrm{24}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow{S}=\left(−\mathrm{1}/\mathrm{8}\right) \\ $$
