Question Number 60155 by Tawa1 last updated on 18/May/19
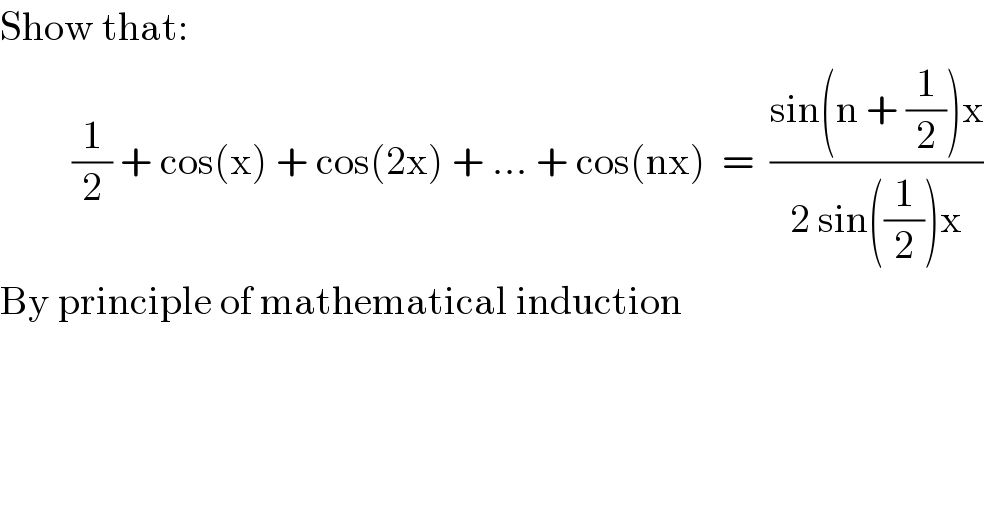
$$\mathrm{Show}\:\mathrm{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{cos}\left(\mathrm{x}\right)\:+\:\mathrm{cos}\left(\mathrm{2x}\right)\:+\:…\:+\:\mathrm{cos}\left(\mathrm{nx}\right)\:\:=\:\:\frac{\mathrm{sin}\left(\mathrm{n}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}}{\mathrm{2}\:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}} \\ $$$$\mathrm{By}\:\mathrm{principle}\:\mathrm{of}\:\mathrm{mathematical}\:\mathrm{induction} \\ $$
Answered by Kunal12588 last updated on 18/May/19
![P(n):(1/2) + cos(x) + cos(2x) + ... + cos(nx) = ((sin(n + (1/2))x)/(2 sin((1/2))x)) P(1): LHS=(1/2)+cos(x)=((1+2cos(x))/2)=((1+2(1−2sin^2 (x/2)))/2) =((3−4sin^2 (x/2))/2) RHS=((sin(1+(1/2))x)/(2sin((1/2))x))=((3sin((1/2))x−4sin^3 ((1/2))x)/(2sin((1/2))x))=((3−4sin^2 (x/2))/2) ⇒LHS=RHS ∴P(1) is true Let P(k) be true for k∈N P(k)(1/2)+cos(x)+cos(2x)+...+cos(kx)=((sin(k+(1/2))x)/(2sin((1/2))x)) (1) Now P(k+1):(1/2)+cos(x)+cos(2x)+...+cos(kx)+cos((k+1)x) =((sin(k+(1/2))x)/(2sin((1/2))x))+cos((k+1)x) [from 1] =((sin(k+(1/2))x+2sin((1/2))xcos((k+1)x))/(2sin((1/2))x)) =((sin(k+(1/2))x+sin(k+1+(1/2))x+sin((1/2)−k−1)x)/(2sin((1/2))x)) =((sin(k+(1/2))x+sin(k+1+(1/2))x−sin(k+(1/2))x)/(2sin((1/2))x)) =((sin(k+1+(1/2))x)/(2sin((1/2))x)) ∴ P(n) is true from Principle of mathematical induction](https://www.tinkutara.com/question/Q60160.png)
$$\:{P}\left({n}\right):\frac{\mathrm{1}}{\mathrm{2}}\:+\:\mathrm{cos}\left(\mathrm{x}\right)\:+\:\mathrm{cos}\left(\mathrm{2x}\right)\:+\:…\:+\:\mathrm{cos}\left(\mathrm{nx}\right)\:\:=\:\:\frac{\mathrm{sin}\left(\mathrm{n}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}}{\mathrm{2}\:\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{x}} \\ $$$${P}\left(\mathrm{1}\right): \\ $$$${LHS}=\frac{\mathrm{1}}{\mathrm{2}}+{cos}\left({x}\right)=\frac{\mathrm{1}+\mathrm{2}{cos}\left({x}\right)}{\mathrm{2}}=\frac{\mathrm{1}+\mathrm{2}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}} \\ $$$${RHS}=\frac{{sin}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}=\frac{\mathrm{3}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}−\mathrm{4}{sin}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}=\frac{\mathrm{3}−\mathrm{4}{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\mathrm{2}} \\ $$$$\Rightarrow{LHS}={RHS} \\ $$$$\therefore{P}\left(\mathrm{1}\right)\:{is}\:{true} \\ $$$${Let}\:{P}\left({k}\right)\:{be}\:{true}\:{for}\:{k}\in{N} \\ $$$${P}\left({k}\right)\frac{\mathrm{1}}{\mathrm{2}}+{cos}\left({x}\right)+{cos}\left(\mathrm{2}{x}\right)+…+{cos}\left({kx}\right)=\frac{{sin}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}\:\:\:\:\left(\mathrm{1}\right) \\ $$$${Now}\: \\ $$$${P}\left({k}+\mathrm{1}\right):\frac{\mathrm{1}}{\mathrm{2}}+{cos}\left({x}\right)+{cos}\left(\mathrm{2}{x}\right)+…+{cos}\left({kx}\right)+{cos}\left(\left({k}+\mathrm{1}\right){x}\right) \\ $$$$=\frac{{sin}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}}+{cos}\left(\left({k}+\mathrm{1}\right){x}\right)\:\:\left[{from}\:\mathrm{1}\right] \\ $$$$=\frac{{sin}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}+\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){xcos}\left(\left({k}+\mathrm{1}\right){x}\right)}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$=\frac{{sin}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}+{sin}\left({k}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}+{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}−{k}−\mathrm{1}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$=\frac{{sin}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}+{sin}\left({k}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}−{sin}\left({k}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$=\frac{{sin}\left({k}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right){x}}{\mathrm{2}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){x}} \\ $$$$\therefore\:{P}\left({n}\right)\:{is}\:{true}\:{from}\:{Principle}\:{of}\:{mathematical}\:{induction} \\ $$
Commented by Tawa1 last updated on 18/May/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 18/May/19
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time} \\ $$
