Question Number 45440 by Rio Michael last updated on 13/Oct/18
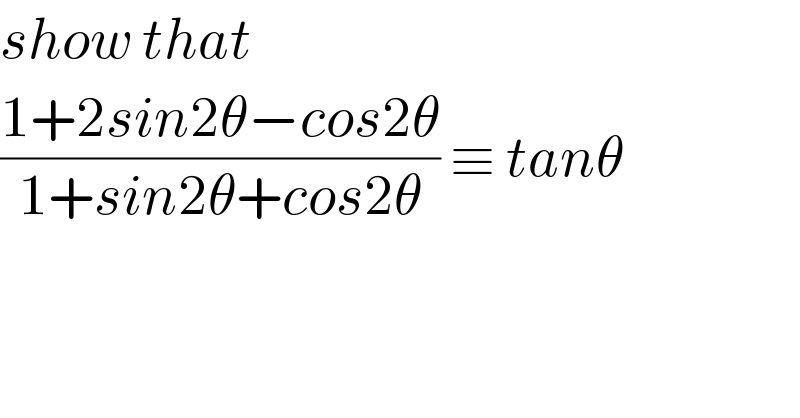
$${show}\:{that}\: \\ $$$$\frac{\mathrm{1}+\mathrm{2}{sin}\mathrm{2}\theta−{cos}\mathrm{2}\theta}{\mathrm{1}+{sin}\mathrm{2}\theta+{cos}\mathrm{2}\theta}\:\equiv\:{tan}\theta \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Oct/18

$$\frac{\mathrm{1}−{cos}\mathrm{2}\theta+{sin}\mathrm{2}\theta}{\mathrm{1}+{cos}\mathrm{2}\theta+{sin}\mathrm{2}\theta} \\ $$$$\frac{\mathrm{2}{sin}^{\mathrm{2}} \theta+\mathrm{2}{sin}\theta{cos}\theta}{\mathrm{2}{cos}^{\mathrm{2}} \theta+\mathrm{2}{sin}\theta{cos}\theta} \\ $$$$\frac{\mathrm{2}{sin}\theta\left({sin}\theta+{cos}\theta\right)}{\mathrm{2}{cos}\theta\left({cos}\theta+{sin}\theta\right)} \\ $$$$={tan}\theta \\ $$
