Question Number 96479 by M±th+et+s last updated on 01/Jun/20
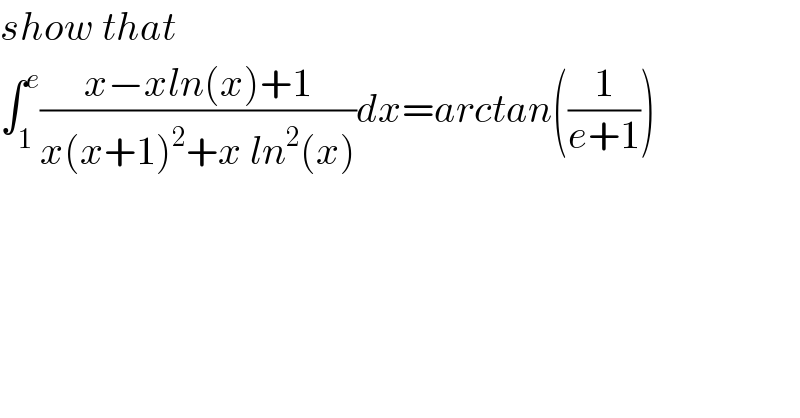
$${show}\:{that} \\ $$$$\int_{\mathrm{1}} ^{{e}} \frac{{x}−{xln}\left({x}\right)+\mathrm{1}}{{x}\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{x}\:{ln}^{\mathrm{2}} \left({x}\right)}{dx}={arctan}\left(\frac{\mathrm{1}}{{e}+\mathrm{1}}\right) \\ $$
Answered by Sourav mridha last updated on 01/Jun/20
![let ln(x)=u,then ∫_0 ^1 (((e^u −ue^u +1))/((e^u +1)^2 +u^2 ))du =−∫_0 ^1 ((d(((e^u +1)/u)))/((((e^u +1)/u))^2 +1^2 ))=−[tan^(−1) ((((e^u +1)/u)/1))]_0 ^1 =−tan^(−1) (e+1)+(𝛑/2)=tan^(−1) [(1/(e+1))]](https://www.tinkutara.com/question/Q96482.png)
$$\boldsymbol{{let}}\:\boldsymbol{{ln}}\left(\boldsymbol{{x}}\right)=\boldsymbol{{u}},\boldsymbol{{then}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\boldsymbol{{e}}^{\boldsymbol{{u}}} −\boldsymbol{{ue}}^{\boldsymbol{{u}}} +\mathrm{1}\right)}{\left(\boldsymbol{{e}}^{\boldsymbol{{u}}} +\mathrm{1}\right)^{\mathrm{2}} +\boldsymbol{{u}}^{\mathrm{2}} }\boldsymbol{{du}} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{d}}\left(\frac{\boldsymbol{{e}}^{\boldsymbol{{u}}} +\mathrm{1}}{\boldsymbol{{u}}}\right)}{\left(\frac{\boldsymbol{{e}}^{\boldsymbol{{u}}} +\mathrm{1}}{\boldsymbol{{u}}}\right)^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }=−\left[\mathrm{tan}^{−\mathrm{1}} \left(\frac{\frac{\boldsymbol{{e}}^{\boldsymbol{{u}}} +\mathrm{1}}{\boldsymbol{{u}}}}{\mathrm{1}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\mathrm{tan}^{−\mathrm{1}} \left(\boldsymbol{{e}}+\mathrm{1}\right)+\frac{\boldsymbol{\pi}}{\mathrm{2}}=\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{1}}{\boldsymbol{{e}}+\mathrm{1}}\right] \\ $$
Commented by M±th+et+s last updated on 01/Jun/20

$${genius}\:{i}\:{am}\:{very}\:{impressed}\:{with}\:{your} \\ $$$${works}\:{in}\:{the}\:{forum} \\ $$
Commented by Sourav mridha last updated on 01/Jun/20
thank you very much
