Question Number 167928 by Mastermind last updated on 29/Mar/22
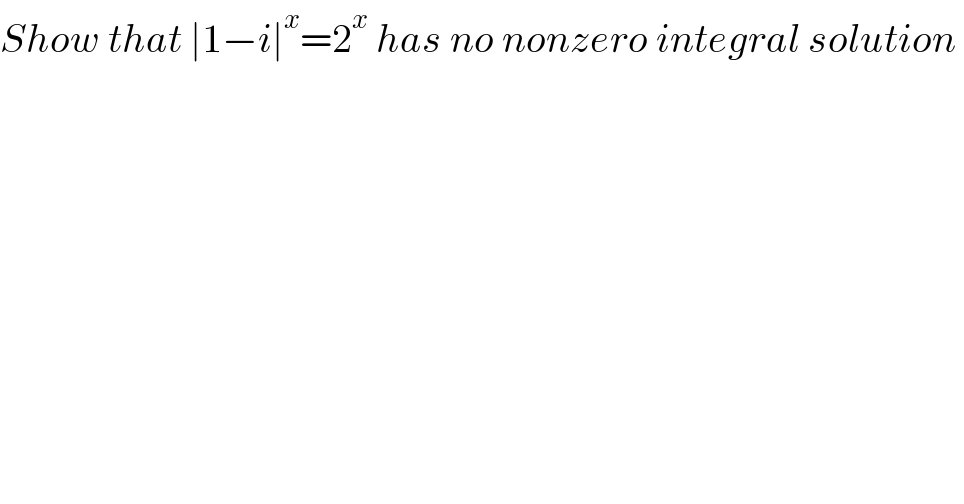
$${Show}\:{that}\:\mid\mathrm{1}−{i}\mid^{{x}} =\mathrm{2}^{{x}} \:{has}\:{no}\:{nonzero}\:{integral}\:{solution}\: \\ $$
Answered by MJS_new last updated on 30/Mar/22
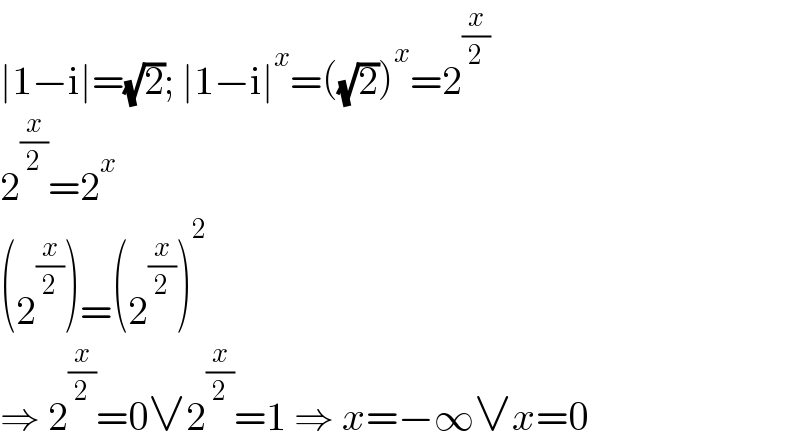
$$\mid\mathrm{1}−\mathrm{i}\mid=\sqrt{\mathrm{2}};\:\mid\mathrm{1}−\mathrm{i}\mid^{{x}} =\left(\sqrt{\mathrm{2}}\right)^{{x}} =\mathrm{2}^{\frac{{x}}{\mathrm{2}}} \\ $$$$\mathrm{2}^{\frac{{x}}{\mathrm{2}}} =\mathrm{2}^{{x}} \\ $$$$\left(\mathrm{2}^{\frac{{x}}{\mathrm{2}}} \right)=\left(\mathrm{2}^{\frac{{x}}{\mathrm{2}}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{2}^{\frac{{x}}{\mathrm{2}}} =\mathrm{0}\vee\mathrm{2}^{\frac{{x}}{\mathrm{2}}} =\mathrm{1}\:\Rightarrow\:{x}=−\infty\vee{x}=\mathrm{0} \\ $$
Commented by Mastermind last updated on 31/Mar/22

$${Thanks} \\ $$
