show-that-2tan-1-2-tan-1-3-tan-1-1-3-

Question Number 34646 by JOHNMASANJA last updated on 09/May/18

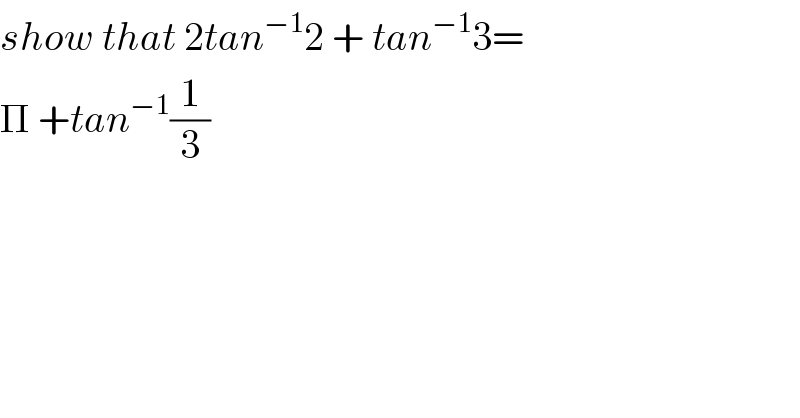
show that 2tan^(−1) 2 + tan^(−1) 3= Π +tan^(−1) (1/3)

$${show}\:{that}\:\mathrm{2}{tan}^{−\mathrm{1}} \mathrm{2}\:+\:{tan}^{−\mathrm{1}} \mathrm{3}= \\ $$$$\Pi\:+{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$

Answered by ajfour last updated on 09/May/18

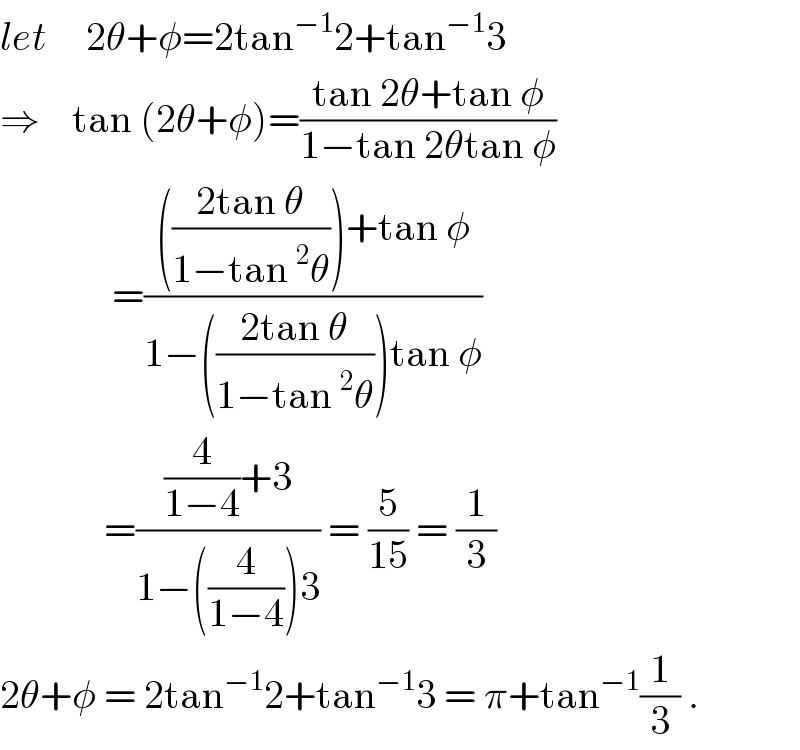
let 2θ+φ=2tan^(−1) 2+tan^(−1) 3 ⇒ tan (2θ+φ)=((tan 2θ+tan φ)/(1−tan 2θtan φ)) =(((((2tan θ)/(1−tan^2 θ)))+tan φ)/(1−(((2tan θ)/(1−tan^2 θ)))tan φ)) =(((4/(1−4))+3)/(1−((4/(1−4)))3)) = (5/(15)) = (1/3) 2θ+φ = 2tan^(−1) 2+tan^(−1) 3 = π+tan^(−1) (1/3) .

$${let}\:\:\:\:\:\mathrm{2}\theta+\phi=\mathrm{2tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{tan}^{−\mathrm{1}} \mathrm{3} \\ $$$$\Rightarrow\:\:\:\:\mathrm{tan}\:\left(\mathrm{2}\theta+\phi\right)=\frac{\mathrm{tan}\:\mathrm{2}\theta+\mathrm{tan}\:\phi}{\mathrm{1}−\mathrm{tan}\:\mathrm{2}\theta\mathrm{tan}\:\phi} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\left(\frac{\mathrm{2tan}\:\theta}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta}\right)+\mathrm{tan}\:\phi}{\mathrm{1}−\left(\frac{\mathrm{2tan}\:\theta}{\mathrm{1}−\mathrm{tan}\:^{\mathrm{2}} \theta}\right)\mathrm{tan}\:\phi} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\frac{\mathrm{4}}{\mathrm{1}−\mathrm{4}}+\mathrm{3}}{\mathrm{1}−\left(\frac{\mathrm{4}}{\mathrm{1}−\mathrm{4}}\right)\mathrm{3}}\:=\:\frac{\mathrm{5}}{\mathrm{15}}\:=\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{2}\theta+\phi\:=\:\mathrm{2tan}^{−\mathrm{1}} \mathrm{2}+\mathrm{tan}^{−\mathrm{1}} \mathrm{3}\:=\:\pi+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\:. \\ $$

Commented by JOHNMASANJA last updated on 09/May/18

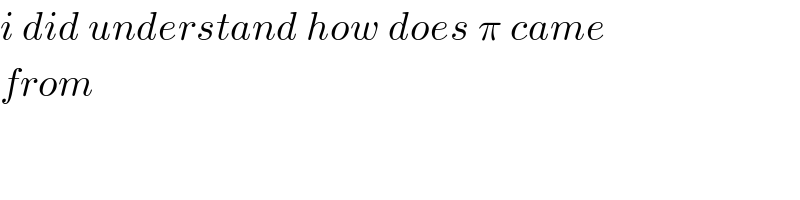
$${i}\:{did}\:{understand}\:{how}\:{does}\:\pi\:{came}\: \\ $$$${from} \\ $$

Facebook Tweet Pin

show-that-2tan-1-2-tan-1-3-tan-1-1-3-

Leave a Reply Cancel reply