Question Number 89906 by Ar Brandon last updated on 19/Apr/20
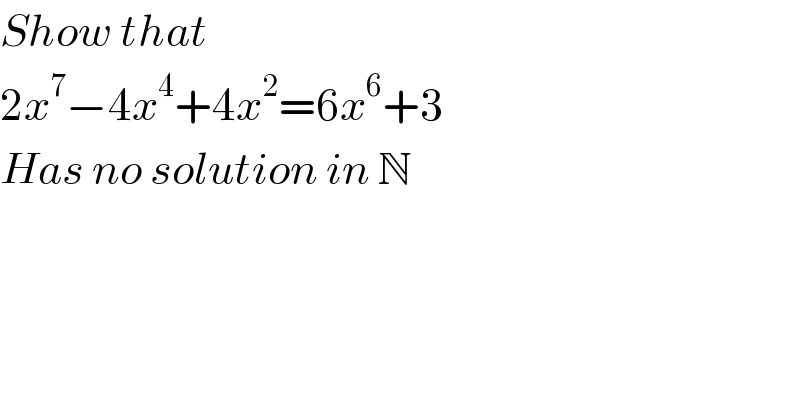
$${Show}\:{that}\: \\ $$$$\mathrm{2}{x}^{\mathrm{7}} −\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} =\mathrm{6}{x}^{\mathrm{6}} +\mathrm{3} \\ $$$${Has}\:{no}\:{solution}\:{in}\:\mathbb{N} \\ $$
Answered by MJS last updated on 20/Apr/20
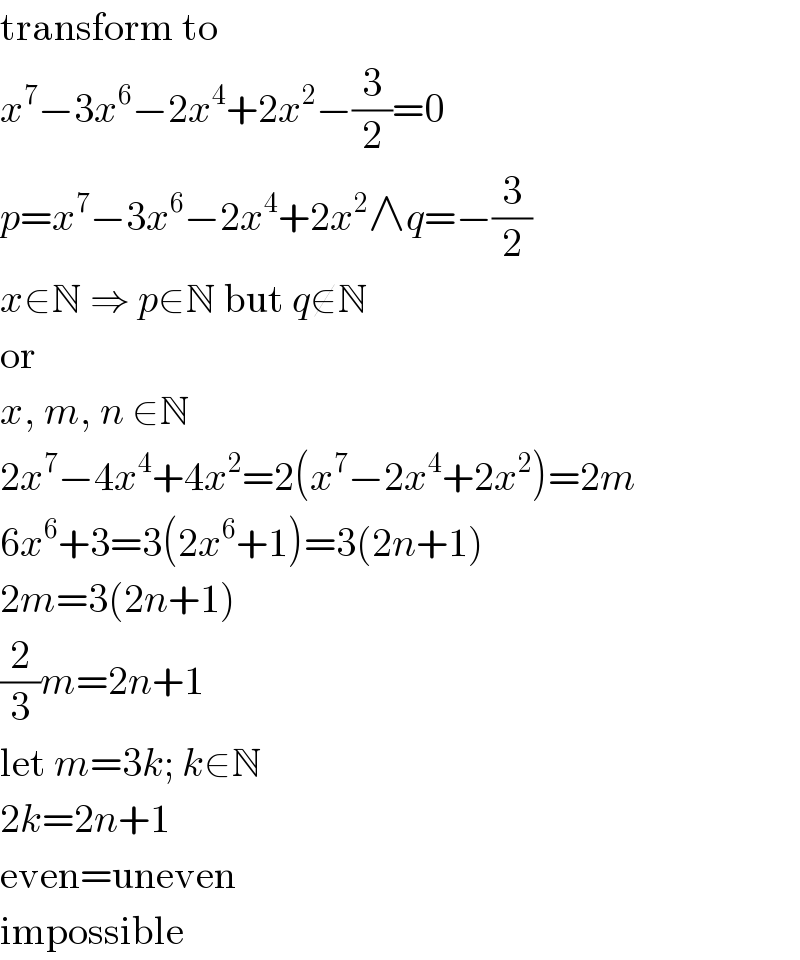
$$\mathrm{transform}\:\mathrm{to} \\ $$$${x}^{\mathrm{7}} −\mathrm{3}{x}^{\mathrm{6}} −\mathrm{2}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{0} \\ $$$${p}={x}^{\mathrm{7}} −\mathrm{3}{x}^{\mathrm{6}} −\mathrm{2}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} \wedge{q}=−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${x}\in\mathbb{N}\:\Rightarrow\:{p}\in\mathbb{N}\:\mathrm{but}\:{q}\notin\mathbb{N} \\ $$$$\mathrm{or} \\ $$$${x},\:{m},\:{n}\:\in\mathbb{N} \\ $$$$\mathrm{2}{x}^{\mathrm{7}} −\mathrm{4}{x}^{\mathrm{4}} +\mathrm{4}{x}^{\mathrm{2}} =\mathrm{2}\left({x}^{\mathrm{7}} −\mathrm{2}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} \right)=\mathrm{2}{m} \\ $$$$\mathrm{6}{x}^{\mathrm{6}} +\mathrm{3}=\mathrm{3}\left(\mathrm{2}{x}^{\mathrm{6}} +\mathrm{1}\right)=\mathrm{3}\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\mathrm{2}{m}=\mathrm{3}\left(\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$\frac{\mathrm{2}}{\mathrm{3}}{m}=\mathrm{2}{n}+\mathrm{1} \\ $$$$\mathrm{let}\:{m}=\mathrm{3}{k};\:{k}\in\mathbb{N} \\ $$$$\mathrm{2}{k}=\mathrm{2}{n}+\mathrm{1} \\ $$$$\mathrm{even}=\mathrm{uneven} \\ $$$$\mathrm{impossible} \\ $$
Commented by Ar Brandon last updated on 20/Apr/20

$${Thank}\:{you}\:{Sir} \\ $$
