Question Number 39586 by Rio Mike last updated on 08/Jul/18
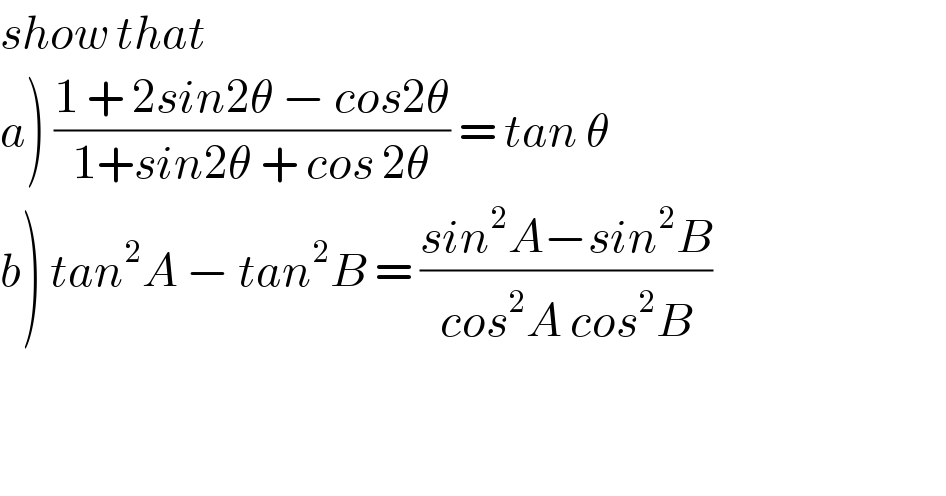
$${show}\:{that}\: \\ $$$$\left.{a}\right)\:\frac{\mathrm{1}\:+\:\mathrm{2}{sin}\mathrm{2}\theta\:−\:{cos}\mathrm{2}\theta}{\mathrm{1}+{sin}\mathrm{2}\theta\:+\:{cos}\:\mathrm{2}\theta}\:=\:{tan}\:\theta \\ $$$$\left.{b}\right)\:{tan}^{\mathrm{2}} {A}\:−\:{tan}^{\mathrm{2}} {B}\:=\:\frac{{sin}^{\mathrm{2}} {A}−{sin}^{\mathrm{2}} {B}}{{cos}^{\mathrm{2}} {A}\:{cos}^{\mathrm{2}} {B}} \\ $$$$ \\ $$$$ \\ $$
Answered by Joel579 last updated on 08/Jul/18
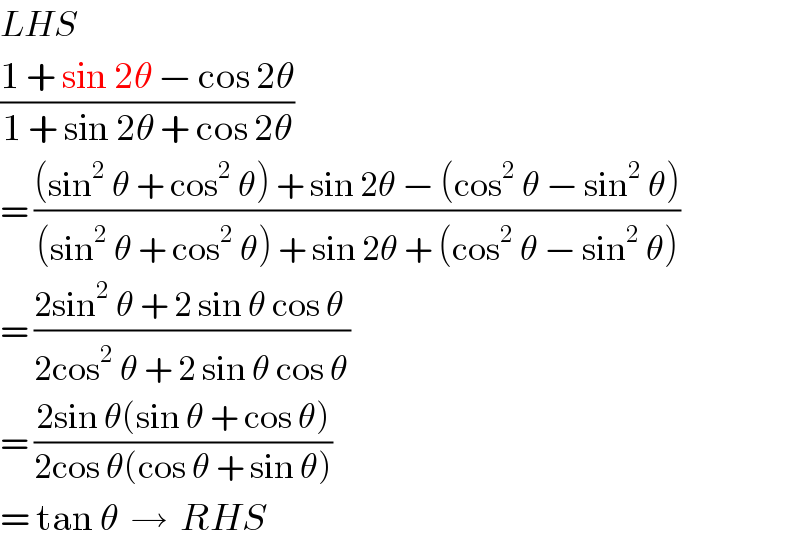
$${LHS} \\ $$$$\frac{\mathrm{1}\:+\:\mathrm{sin}\:\mathrm{2}\theta\:−\:\mathrm{cos}\:\mathrm{2}\theta}{\mathrm{1}\:+\:\mathrm{sin}\:\mathrm{2}\theta\:+\:\mathrm{cos}\:\mathrm{2}\theta} \\ $$$$=\:\frac{\left(\mathrm{sin}^{\mathrm{2}} \:\theta\:+\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)\:+\:\mathrm{sin}\:\mathrm{2}\theta\:−\:\left(\mathrm{cos}^{\mathrm{2}} \:\theta\:−\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)}{\left(\mathrm{sin}^{\mathrm{2}} \:\theta\:+\:\mathrm{cos}^{\mathrm{2}} \:\theta\right)\:+\:\mathrm{sin}\:\mathrm{2}\theta\:+\:\left(\mathrm{cos}^{\mathrm{2}} \:\theta\:−\:\mathrm{sin}^{\mathrm{2}} \:\theta\right)} \\ $$$$=\:\frac{\mathrm{2sin}^{\mathrm{2}} \:\theta\:+\:\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta\:}{\mathrm{2cos}^{\mathrm{2}} \:\theta\:+\:\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$$=\:\frac{\mathrm{2sin}\:\theta\left(\mathrm{sin}\:\theta\:+\:\mathrm{cos}\:\theta\right)}{\mathrm{2cos}\:\theta\left(\mathrm{cos}\:\theta\:+\:\mathrm{sin}\:\theta\right)} \\ $$$$=\:\mathrm{tan}\:\theta\:\:\rightarrow\:\:{RHS} \\ $$
Answered by Joel579 last updated on 08/Jul/18
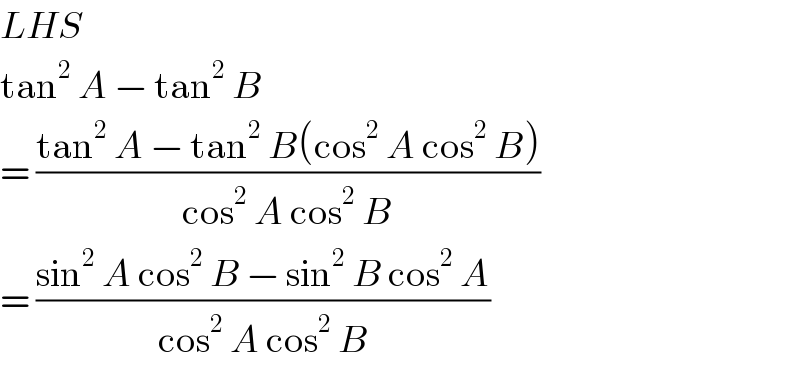
$${LHS}\: \\ $$$$\mathrm{tan}^{\mathrm{2}} \:{A}\:−\:\mathrm{tan}^{\mathrm{2}} \:{B} \\ $$$$=\:\frac{\mathrm{tan}^{\mathrm{2}} \:{A}\:−\:\mathrm{tan}^{\mathrm{2}} \:{B}\left(\mathrm{cos}^{\mathrm{2}} \:{A}\:\mathrm{cos}^{\mathrm{2}} \:{B}\right)}{\mathrm{cos}^{\mathrm{2}} \:{A}\:\mathrm{cos}^{\mathrm{2}} \:{B}} \\ $$$$=\:\frac{\mathrm{sin}^{\mathrm{2}} \:{A}\:\mathrm{cos}^{\mathrm{2}} \:{B}\:−\:\mathrm{sin}^{\mathrm{2}} \:{B}\:\mathrm{cos}^{\mathrm{2}} \:{A}}{\mathrm{cos}^{\mathrm{2}} \:{A}\:\mathrm{cos}^{\mathrm{2}} \:{B}} \\ $$
