Menu Close

show-that-a-1-cos2A-1-cos2A-tan-2-A-b-sin2A-1-cos2A-tanA-

Tinku Tara 0 Comments
Pin




Question Number 41394 by Rio Michael last updated on 07/Aug/18
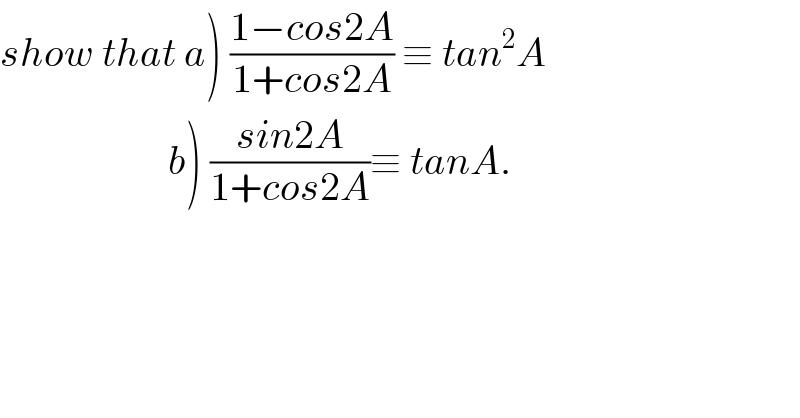
show that a) ((1−cos2A)/(1+cos2A)) ≡ tan^2 A b) ((sin2A)/(1+cos2A))≡ tanA.
$$\left.{show}\:{that}\:{a}\right)\:\frac{\mathrm{1}−{cos}\mathrm{2}{A}}{\mathrm{1}+{cos}\mathrm{2}{A}}\:\equiv\:{tan}^{\mathrm{2}} {A} \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}\right)\:\frac{{sin}\mathrm{2}{A}}{\mathrm{1}+{cos}\mathrm{2}{A}}\equiv\:{tanA}. \\ $$
Commented by mondodotto@gmail.com last updated on 07/Aug/18
in part B it should be proved to tanA not tan2A
$$\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{part}}\:\boldsymbol{\mathrm{B}}\:\boldsymbol{\mathrm{it}}\:\boldsymbol{\mathrm{should}}\:\boldsymbol{\mathrm{be}}\:\boldsymbol{\mathrm{proved}} \\ $$$$\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{tanA}}\:\boldsymbol{\mathrm{not}}\:\boldsymbol{\mathrm{tan}}\mathrm{2}\boldsymbol{\mathrm{A}} \\ $$
Answered by alex041103 last updated on 06/Aug/18
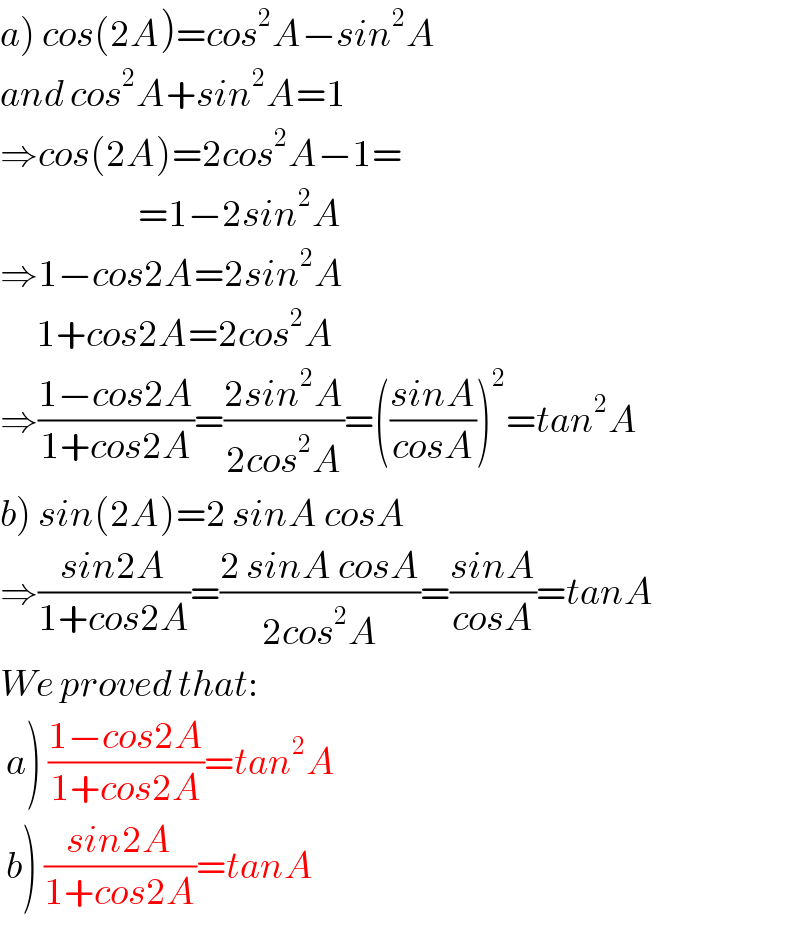
a) cos(2A)=cos^2 A−sin^2 A and cos^2 A+sin^2 A=1 ⇒cos(2A)=2cos^2 A−1= =1−2sin^2 A ⇒1−cos2A=2sin^2 A 1+cos2A=2cos^2 A ⇒((1−cos2A)/(1+cos2A))=((2sin^2 A)/(2cos^2 A))=(((sinA)/(cosA)))^2 =tan^2 A b) sin(2A)=2 sinA cosA ⇒((sin2A)/(1+cos2A))=((2 sinA cosA)/(2cos^2 A))=((sinA)/(cosA))=tanA We proved that: a) ((1−cos2A)/(1+cos2A))=tan^2 A b) ((sin2A)/(1+cos2A))=tanA
$$\left.{a}\right)\:{cos}\left(\mathrm{2}{A}\right)={cos}^{\mathrm{2}} {A}−{sin}^{\mathrm{2}} {A} \\ $$$${and}\:{cos}^{\mathrm{2}} {A}+{sin}^{\mathrm{2}} {A}=\mathrm{1} \\ $$$$\Rightarrow{cos}\left(\mathrm{2}{A}\right)=\mathrm{2}{cos}^{\mathrm{2}} {A}−\mathrm{1}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} {A} \\ $$$$\Rightarrow\mathrm{1}−{cos}\mathrm{2}{A}=\mathrm{2}{sin}^{\mathrm{2}} {A} \\ $$$$\:\:\:\:\:\:\mathrm{1}+{cos}\mathrm{2}{A}=\mathrm{2}{cos}^{\mathrm{2}} {A} \\ $$$$\Rightarrow\frac{\mathrm{1}−{cos}\mathrm{2}{A}}{\mathrm{1}+{cos}\mathrm{2}{A}}=\frac{\mathrm{2}{sin}^{\mathrm{2}} {A}}{\mathrm{2}{cos}^{\mathrm{2}} {A}}=\left(\frac{{sinA}}{{cosA}}\right)^{\mathrm{2}} ={tan}^{\mathrm{2}} {A} \\ $$$$\left.{b}\right)\:{sin}\left(\mathrm{2}{A}\right)=\mathrm{2}\:{sinA}\:{cosA} \\ $$$$\Rightarrow\frac{{sin}\mathrm{2}{A}}{\mathrm{1}+{cos}\mathrm{2}{A}}=\frac{\mathrm{2}\:{sinA}\:{cosA}}{\mathrm{2}{cos}^{\mathrm{2}} {A}}=\frac{{sinA}}{{cosA}}={tanA} \\ $$$${We}\:{proved}\:{that}: \\ $$$$\left.\:{a}\right)\:\frac{\mathrm{1}−{cos}\mathrm{2}{A}}{\mathrm{1}+{cos}\mathrm{2}{A}}={tan}^{\mathrm{2}} {A} \\ $$$$\left.\:{b}\right)\:\frac{{sin}\mathrm{2}{A}}{\mathrm{1}+{cos}\mathrm{2}{A}}={tanA} \\ $$
Commented by alex041103 last updated on 06/Aug/18
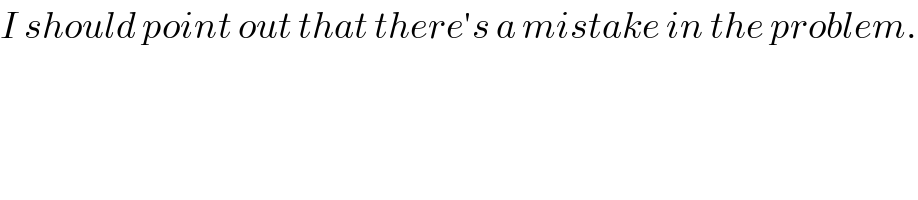
I should point out that there′s a mistake in the problem.
$${I}\:{should}\:{point}\:{out}\:{that}\:{there}'{s}\:{a}\:{mistake}\:{in}\:{the}\:{problem}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *