Menu Close

Show-that-a-b-2-2-a-2-b-2-

Tinku Tara 0 Comments
Pin




Question Number 49604 by Tawa1 last updated on 08/Dec/18
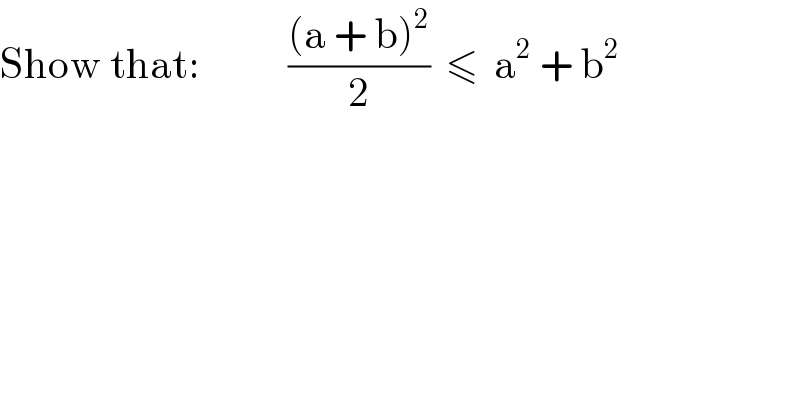
Show that: (((a + b)^2 )/2) ≤ a^2 + b^2
$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\:\:\:\:\:\:\:\frac{\left(\mathrm{a}\:+\:\mathrm{b}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\leqslant\:\:\mathrm{a}^{\mathrm{2}} \:+\:\mathrm{b}^{\mathrm{2}} \\ $$
Answered by afachri last updated on 08/Dec/18
let (a − b)^2 ≥ 0 a^2 − 2ab + b^2 ≥ 0 a^2 + b^2 ≥ 2ab a^2 + 2ab + b^2 ≥ 2ab + 2ab (a + b)^2 ≥ 4(ab) meanwhile : ab = (( (a + b)^2 − (a^2 + b^2 ) )/2) (a + b)^2 ≥ 4((( (a + b)^2 − (a^2 + b^2 ))/2)) (a + b)^(2 ) ≥ 2(a + b)^2 − 2(a^2 + b^2 )] −(a + b)^2 ≥ −2(a^2 + b^2 ) (((a + b)^2 )/2) ≤ (a^2 + b^2 )
$$\mathrm{let}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:−\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} −\:\mathrm{2}{ab}\:+\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} \:+\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{2}{ab} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} +\:\mathrm{2}{ab}\:+\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{2}{ab}\:+\:\mathrm{2}{ab} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:\mathrm{4}\left({ab}\right) \\ $$$$ \\ $$$$\mathrm{meanwhile}\:\::\:\:{ab}\:\:=\:\:\frac{\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:−\:\:\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right)\:}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:\:\mathrm{4}\left(\frac{\:\left({a}\:+\:{b}\right)^{\mathrm{2}} \:−\:\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right)}{\mathrm{2}}\right) \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}\:+\:{b}\right)^{\mathrm{2}\:} \:\geqslant\:\:\mathrm{2}\left({a}\:+\:{b}\right)^{\mathrm{2}} \:−\:\mathrm{2}\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:−\left({a}\:+\:{b}\right)^{\mathrm{2}} \:\:\geqslant\:\:−\mathrm{2}\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\left({a}\:+\:{b}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\leqslant\:\:\left({a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \right) \\ $$$$ \\ $$
Commented by Tawa1 last updated on 08/Dec/18
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\: \\ $$
Commented by Tawa1 last updated on 08/Dec/18
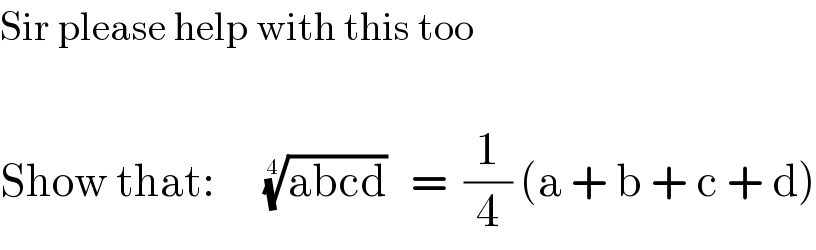
Sir please help with this too Show that: ((abcd))^(1/4) = (1/4) (a + b + c + d)
$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{help}\:\mathrm{with}\:\mathrm{this}\:\mathrm{too} \\ $$$$ \\ $$$$\mathrm{Show}\:\mathrm{that}:\:\:\:\:\:\:\sqrt[{\mathrm{4}}]{\mathrm{abcd}}\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\left(\mathrm{a}\:+\:\mathrm{b}\:+\:\mathrm{c}\:+\:\mathrm{d}\right) \\ $$
Commented by afachri last updated on 08/Dec/18
Arithmaric Mean = ((a + b + c + d)/4) Geometric Mean = ((abcd^ ))^(1/4) Arithmatic Mean ≥ Geometric Mean (1/4)(a + b + c + d) ≥ ((abcd^ ))^(1/4) so, the equalty can be achieved only and if only : a = b= c = d then (1/4)(a + b + c + d) = ((abcd^ ))^(1/4)
$$\:\:\mathrm{Arithmaric}\:\mathrm{Mean}\:=\:\:\frac{{a}\:+\:{b}\:+\:{c}\:+\:{d}}{\mathrm{4}} \\ $$$$\:\:\mathrm{Geometric}\:\mathrm{Mean}\:\:=\:\:\sqrt[{\mathrm{4}}]{{abcd}^{} } \\ $$$$ \\ $$$$\:\:\mathrm{Arithmatic}\:\mathrm{Mean}\:\:\geqslant\:\:\mathrm{Geometric}\:\mathrm{Mean} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\left({a}\:+\:{b}\:+\:{c}\:+\:{d}\right)\:\:\geqslant\:\:\sqrt[{\mathrm{4}}]{{abcd}^{} }\: \\ $$$$\:\:\mathrm{so},\:\mathrm{the}\:\mathrm{equalty}\:\mathrm{can}\:\mathrm{be}\:\mathrm{achieved}\:\mathrm{only} \\ $$$$\:\:\mathrm{and}\:\mathrm{if}\:\mathrm{only}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}\:=\:{b}=\:{c}\:=\:{d} \\ $$$$\:\:\mathrm{then}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\left({a}\:+\:{b}\:+\:{c}\:+\:{d}\right)\:\:=\:\:\sqrt[{\mathrm{4}}]{{abcd}^{} }\: \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa1 last updated on 08/Dec/18
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by afachri last updated on 08/Dec/18
ur welcome, Sir. Pardon me, are u an Indonesian ?
$$\mathrm{ur}\:\mathrm{welcome},\:\mathrm{Sir}. \\ $$$$\mathrm{Pardon}\:\mathrm{me},\:\mathrm{are}\:\mathrm{u}\:\mathrm{an}\:\mathrm{Indonesian}\:? \\ $$
Commented by Tawa1 last updated on 08/Dec/18
No sir
$$\mathrm{No}\:\mathrm{sir} \\ $$
Commented by afachri last updated on 08/Dec/18
nevermind Sir. i′m just asking Sir. :)
$$\mathrm{nevermind}\:\mathrm{Sir}. \\ $$$$\left.\mathrm{i}'\mathrm{m}\:\mathrm{just}\:\mathrm{asking}\:\mathrm{Sir}.\::\right) \\ $$
Commented by Tawa1 last updated on 08/Dec/18
Ok sir
$$\mathrm{Ok}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 08/Dec/18
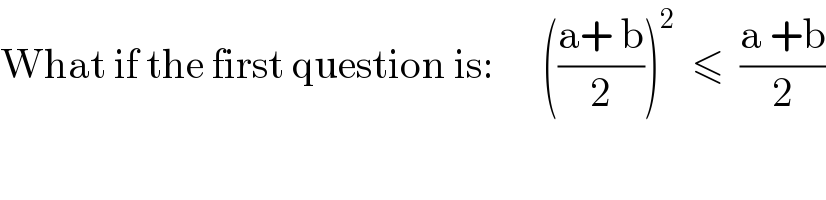
What if the first question is: (((a+ b)/2))^2 ≤ ((a +b)/2)
$$\mathrm{What}\:\mathrm{if}\:\mathrm{the}\:\mathrm{first}\:\mathrm{question}\:\mathrm{is}:\:\:\:\:\:\:\left(\frac{\mathrm{a}+\:\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} \:\:\leqslant\:\:\frac{\mathrm{a}\:+\mathrm{b}}{\mathrm{2}} \\ $$
Commented by Tawa1 last updated on 08/Dec/18
How will the prove be
$$\mathrm{How}\:\mathrm{will}\:\mathrm{the}\:\mathrm{prove}\:\mathrm{be} \\ $$
Commented by afachri last updated on 08/Dec/18
i had given the 2 solutuions earlier Sir. what kind of proof else you sesrching for Sir ?? i′m sorry i don′t get it.
$$\:\:\mathrm{i}\:\mathrm{had}\:\mathrm{given}\:\mathrm{the}\:\mathrm{2}\:\mathrm{solutuions}\:\mathrm{earlier}\:\mathrm{Sir}. \\ $$$$\:\:\mathrm{what}\:\mathrm{kind}\:\mathrm{of}\:\mathrm{proof}\:\mathrm{else}\:\mathrm{you}\:\mathrm{sesrching} \\ $$$$\:\:\mathrm{for}\:\mathrm{Sir}\:??\:\mathrm{i}'\mathrm{m}\:\mathrm{sorry}\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{it}. \\ $$$$ \\ $$
Answered by afachri last updated on 08/Dec/18
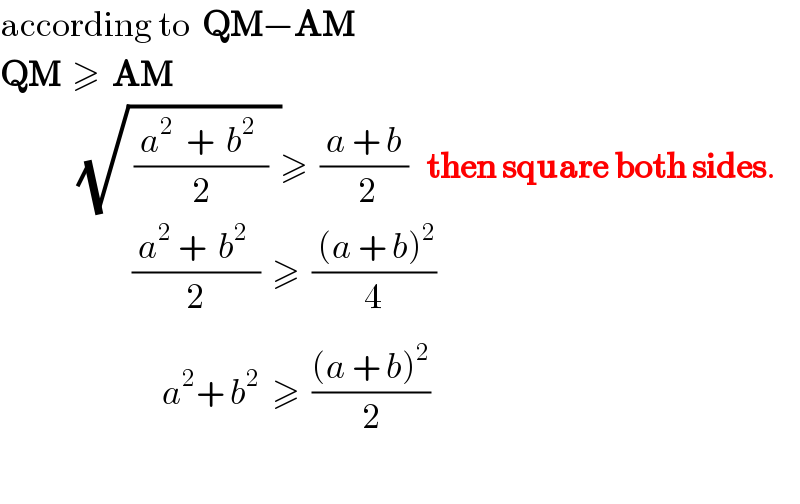
according to QM−AM QM ≥ AM (√( (( a^2^ + b^2 )/2) ))≥ (( a + b )/( 2)) then square both sides. (( a^2 + b^2 )/2) ≥ (( (a + b)^2 )/( 4_ )) a^2 + b^2 ≥ (((a + b)^2 )/2)
$$\mathrm{according}\:\mathrm{to}\:\:\boldsymbol{\mathrm{QM}}−\boldsymbol{\mathrm{AM}} \\ $$$$\boldsymbol{\mathrm{QM}}\:\:\geqslant\:\:\boldsymbol{\mathrm{AM}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{\:\frac{\:{a}^{\mathrm{2}^{} } \:+\:\:{b}^{\mathrm{2}} \:\:}{\mathrm{2}}\:\:}\geqslant\:\:\frac{\:{a}\:+\:{b}\:}{\:\mathrm{2}}\:\:\:\boldsymbol{\mathrm{then}}\:\boldsymbol{\mathrm{square}}\:\boldsymbol{\mathrm{both}}\:\boldsymbol{\mathrm{sides}}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\:{a}^{\mathrm{2}} \:+\:\:{b}^{\mathrm{2}} \:\:}{\mathrm{2}}\:\:\geqslant\:\:\frac{\:\left({a}\:+\:{b}\right)^{\mathrm{2}} }{\:\mathrm{4}_{} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} +\:{b}^{\mathrm{2}} \:\:\geqslant\:\:\frac{\left({a}\:+\:{b}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 08/Dec/18
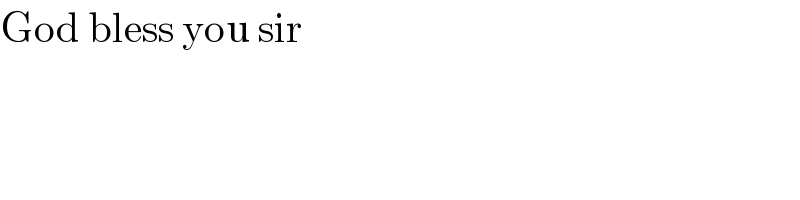
God bless you sir
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by Tawa1 last updated on 08/Dec/18
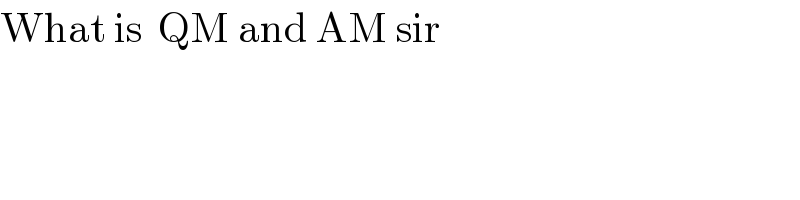
What is QM and AM sir
$$\mathrm{What}\:\mathrm{is}\:\:\mathrm{QM}\:\mathrm{and}\:\mathrm{AM}\:\mathrm{sir} \\ $$
Commented by afachri last updated on 08/Dec/18
you′re welcome,Sir
$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome},\mathrm{Sir} \\ $$
Commented by Tawa1 last updated on 08/Dec/18
???
$$??? \\ $$
Commented by afachri last updated on 08/Dec/18
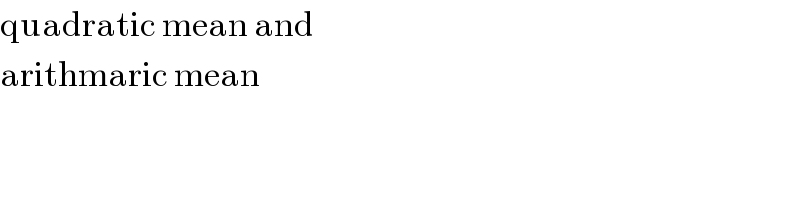
quadratic mean and arithmaric mean
$$\mathrm{quadratic}\:\mathrm{mean}\:\mathrm{and} \\ $$$$\mathrm{arithmaric}\:\mathrm{mean} \\ $$
Commented by Tawa1 last updated on 08/Dec/18
God bless you sir. I really appreciate your time
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$$$ \\ $$
Commented by afachri last updated on 08/Dec/18
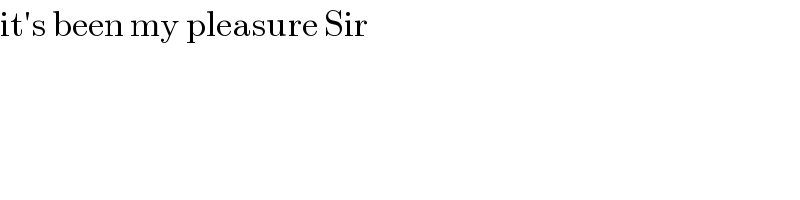
it′s been my pleasure Sir
$$\mathrm{it}'\mathrm{s}\:\mathrm{been}\:\mathrm{my}\:\mathrm{pleasure}\:\mathrm{Sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *