Question Number 17220 by Arnab Maiti last updated on 02/Jul/17
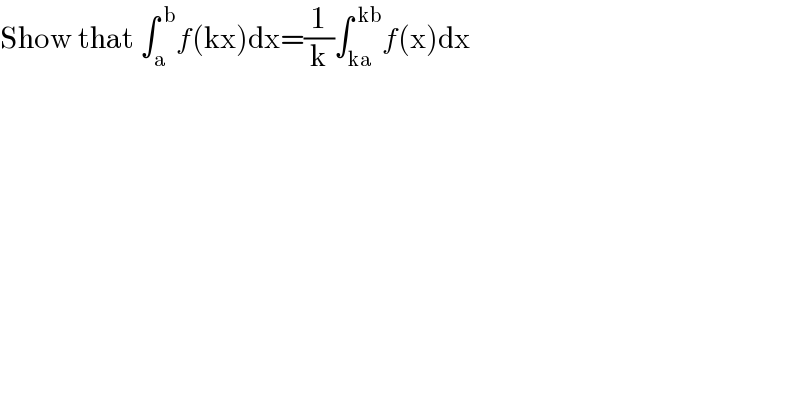
$$\mathrm{Show}\:\mathrm{that}\:\int_{\mathrm{a}} ^{\:\mathrm{b}} {f}\left(\mathrm{kx}\right)\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{k}}\int_{\mathrm{ka}} ^{\:\mathrm{kb}} {f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$
Answered by ajfour last updated on 02/Jul/17
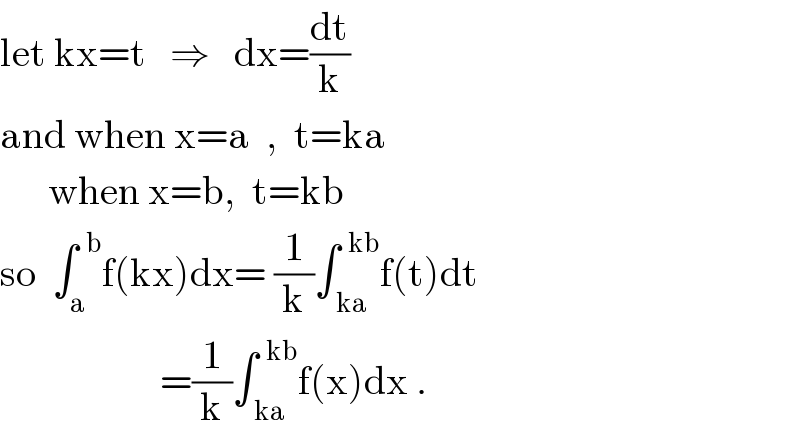
$$\mathrm{let}\:\mathrm{kx}=\mathrm{t}\:\:\:\Rightarrow\:\:\:\mathrm{dx}=\frac{\mathrm{dt}}{\mathrm{k}} \\ $$$$\mathrm{and}\:\mathrm{when}\:\mathrm{x}=\mathrm{a}\:\:,\:\:\mathrm{t}=\mathrm{ka} \\ $$$$\:\:\:\:\:\:\mathrm{when}\:\mathrm{x}=\mathrm{b},\:\:\mathrm{t}=\mathrm{kb} \\ $$$$\mathrm{so}\:\:\int_{\mathrm{a}} ^{\:\:\mathrm{b}} \mathrm{f}\left(\mathrm{kx}\right)\mathrm{dx}=\:\frac{\mathrm{1}}{\mathrm{k}}\int_{\:\mathrm{ka}} ^{\:\:\mathrm{kb}} \mathrm{f}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{k}}\int_{\:\mathrm{ka}} ^{\:\:\mathrm{kb}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:. \\ $$
Commented by Arnab Maiti last updated on 02/Jul/17

$$\mathrm{Thank}\:\mathrm{u}\:\mathrm{sir}. \\ $$
