Question Number 25771 by keyurpatel last updated on 14/Dec/17

$${show}\:{that}\:\frac{\mathrm{cos}\:\mathrm{50}}{\mathrm{sin}\:\mathrm{40}}+\frac{\mathrm{sin}\:\mathrm{42}}{\mathrm{cos}\:\mathrm{48}}−\frac{\mathrm{2tan}\:\mathrm{18}}{\mathrm{cot}\:\mathrm{72}}=\mathrm{0} \\ $$
Answered by deepak123 last updated on 14/Dec/17
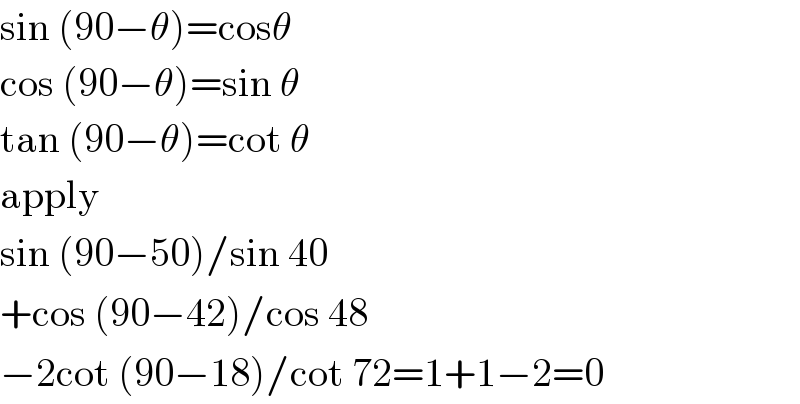
$$\mathrm{sin}\:\left(\mathrm{90}−\theta\right)=\mathrm{cos}\theta \\ $$$$\mathrm{cos}\:\left(\mathrm{90}−\theta\right)=\mathrm{sin}\:\theta \\ $$$$\mathrm{tan}\:\left(\mathrm{90}−\theta\right)=\mathrm{cot}\:\theta \\ $$$$\mathrm{apply} \\ $$$$\mathrm{sin}\:\left(\mathrm{90}−\mathrm{50}\right)/\mathrm{sin}\:\mathrm{40} \\ $$$$+\mathrm{cos}\:\left(\mathrm{90}−\mathrm{42}\right)/\mathrm{cos}\:\mathrm{48} \\ $$$$−\mathrm{2cot}\:\left(\mathrm{90}−\mathrm{18}\right)/\mathrm{cot}\:\mathrm{72}=\mathrm{1}+\mathrm{1}−\mathrm{2}=\mathrm{0} \\ $$
