Question Number 94862 by mathocean1 last updated on 21/May/20
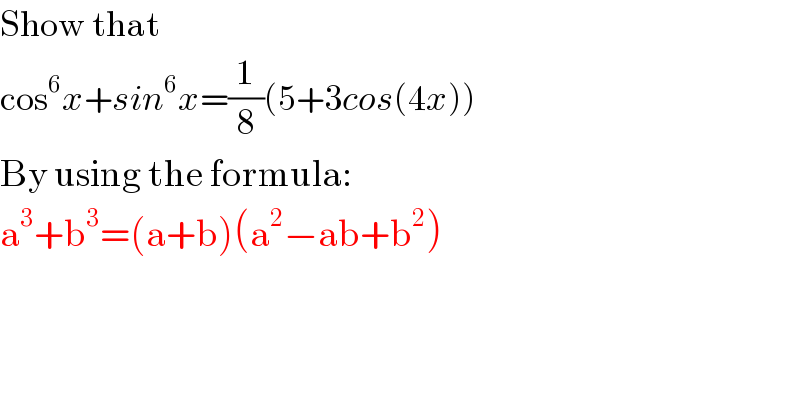
$$\mathrm{Show}\:\mathrm{that}\: \\ $$$$\mathrm{cos}^{\mathrm{6}} {x}+{sin}^{\mathrm{6}} {x}=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{5}+\mathrm{3}{cos}\left(\mathrm{4}{x}\right)\right) \\ $$$$\mathrm{By}\:\mathrm{using}\:\mathrm{the}\:\mathrm{formula}: \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \right) \\ $$
Commented by john santu last updated on 21/May/20
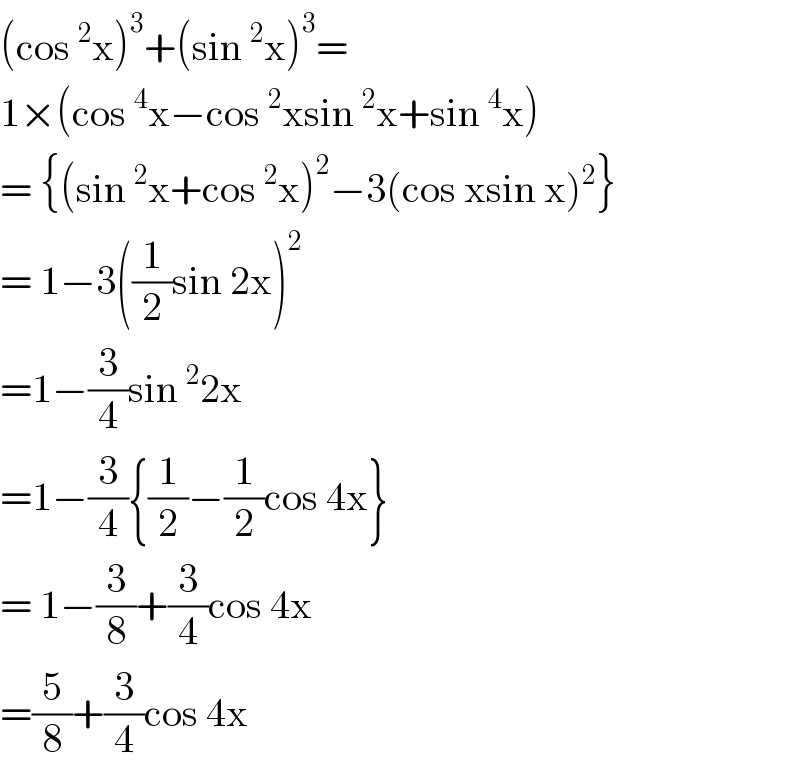
$$\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{3}} +\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{3}} =\: \\ $$$$\mathrm{1}×\left(\mathrm{cos}\:^{\mathrm{4}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \mathrm{xsin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{4}} \mathrm{x}\right) \\ $$$$=\:\left\{\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}\right)^{\mathrm{2}} −\mathrm{3}\left(\mathrm{cos}\:\mathrm{xsin}\:\mathrm{x}\right)^{\mathrm{2}} \right\} \\ $$$$=\:\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2x}\right)^{\mathrm{2}} \\ $$$$=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2x}\: \\ $$$$=\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4x}\right\} \\ $$$$=\:\mathrm{1}−\frac{\mathrm{3}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4x} \\ $$$$=\frac{\mathrm{5}}{\mathrm{8}}+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{cos}\:\mathrm{4x}\: \\ $$
Commented by mathocean1 last updated on 21/May/20

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}! \\ $$
Commented by niroj last updated on 21/May/20
����
Commented by i jagooll last updated on 21/May/20
��������
