Question Number 171596 by nadovic last updated on 18/Jun/22
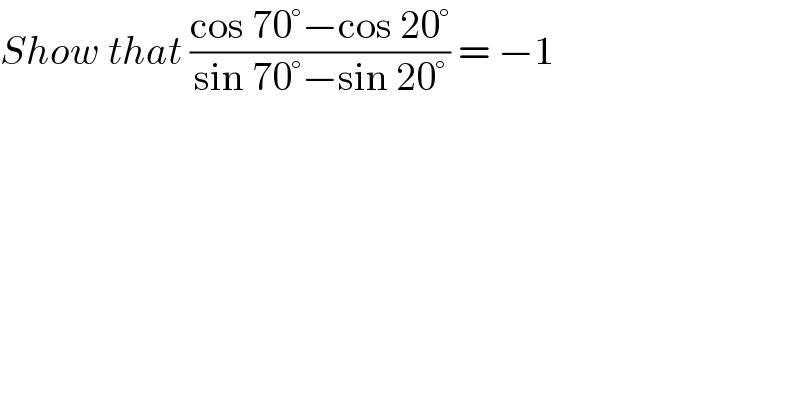
$${Show}\:{that}\:\frac{\mathrm{cos}\:\mathrm{70}°−\mathrm{cos}\:\mathrm{20}°}{\mathrm{sin}\:\mathrm{70}°−\mathrm{sin}\:\mathrm{20}°}\:=\:−\mathrm{1} \\ $$
Commented by mr W last updated on 18/Jun/22
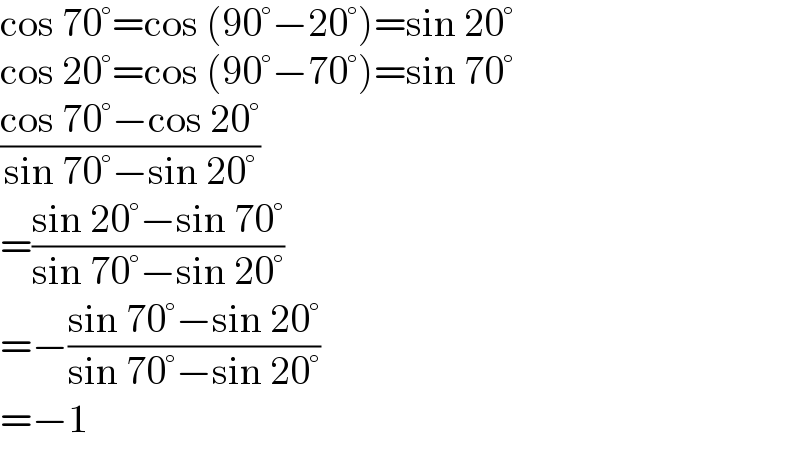
$$\mathrm{cos}\:\mathrm{70}°=\mathrm{cos}\:\left(\mathrm{90}°−\mathrm{20}°\right)=\mathrm{sin}\:\mathrm{20}° \\ $$$$\mathrm{cos}\:\mathrm{20}°=\mathrm{cos}\:\left(\mathrm{90}°−\mathrm{70}°\right)=\mathrm{sin}\:\mathrm{70}° \\ $$$$\frac{\mathrm{cos}\:\mathrm{70}°−\mathrm{cos}\:\mathrm{20}°}{\mathrm{sin}\:\mathrm{70}°−\mathrm{sin}\:\mathrm{20}°}\: \\ $$$$=\frac{\mathrm{sin}\:\mathrm{20}°−\mathrm{sin}\:\mathrm{70}°}{\mathrm{sin}\:\mathrm{70}°−\mathrm{sin}\:\mathrm{20}°}\: \\ $$$$=−\frac{\mathrm{sin}\:\mathrm{70}°−\mathrm{sin}\:\mathrm{20}°}{\mathrm{sin}\:\mathrm{70}°−\mathrm{sin}\:\mathrm{20}°} \\ $$$$=−\mathrm{1} \\ $$
Commented by nadovic last updated on 18/Jun/22

$${Thank}\:{you}\:{Sir} \\ $$
Commented by peter frank last updated on 18/Jun/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by cherokeesay last updated on 18/Jun/22
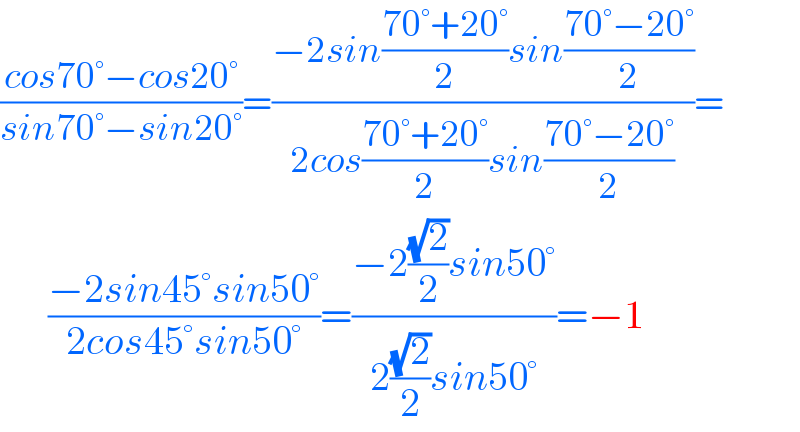
$$\frac{{cos}\mathrm{70}°−{cos}\mathrm{20}°}{{sin}\mathrm{70}°−{sin}\mathrm{20}°}=\frac{−\mathrm{2}{sin}\frac{\mathrm{70}°+\mathrm{20}°}{\mathrm{2}}{sin}\frac{\mathrm{70}°−\mathrm{20}°}{\mathrm{2}}}{\mathrm{2}{cos}\frac{\mathrm{70}°+\mathrm{20}°}{\mathrm{2}}{sin}\frac{\mathrm{70}°−\mathrm{20}°}{\mathrm{2}}}= \\ $$$$\:\:\:\:\:\:\frac{−\mathrm{2}{sin}\mathrm{45}°{sin}\mathrm{50}°}{\mathrm{2}{cos}\mathrm{45}°{sin}\mathrm{50}°}=\frac{−\mathrm{2}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{sin}\mathrm{50}°}{\mathrm{2}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}{sin}\mathrm{50}°}=−\mathrm{1} \\ $$
Commented by nadovic last updated on 18/Jun/22

$${Thank}\:{you}\:{Sir} \\ $$
