Menu Close

show-that-cos-cos2-cos-n-cos-1-2-n-1-sin-1-2-n-sin-1-2-n-Show-that-sin-sin-2-sin-n-sin-1-2-n-1-sin-1-2-n-sin-1-2-n-where-R-and-2pik-k

Tinku Tara 0 Comments
Pin




Question Number 102627 by Rio Michael last updated on 10/Jul/20
show that: cosθ + cos2θ + ....cos nθ= ((cos (1/2)(n +1)θ sin(1/2)nθ)/(sin (1/2)nθ)) Show that: sin θ + sin 2θ + ....+ sin nθ = ((sin (1/2)(n + 1)θ sin(1/2)nθ)/(sin (1/2)nθ)) where θ ∈ R and θ ≠2πk , k ∈Z
$$\mathrm{show}\:\mathrm{that}:\:\mathrm{cos}\theta\:+\:\mathrm{cos2}\theta\:+\:….\mathrm{cos}\:{n}\theta=\:\frac{\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}}\left({n}\:+\mathrm{1}\right)\theta\:\mathrm{sin}\frac{\mathrm{1}}{\mathrm{2}}{n}\theta}{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{n}\theta} \\ $$$$\mathrm{Show}\:\mathrm{that}:\:\mathrm{sin}\:\theta\:+\:\mathrm{sin}\:\mathrm{2}\theta\:+\:….+\:\mathrm{sin}\:{n}\theta\:=\:\frac{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}\left({n}\:+\:\mathrm{1}\right)\theta\:\mathrm{sin}\frac{\mathrm{1}}{\mathrm{2}}{n}\theta}{\mathrm{sin}\:\frac{\mathrm{1}}{\mathrm{2}}{n}\theta} \\ $$$$\mathrm{where}\:\theta\:\in\:\mathbb{R}\:\mathrm{and}\:\theta\:\neq\mathrm{2}\pi{k}\:,\:{k}\:\in\mathbb{Z} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 10/Jul/20
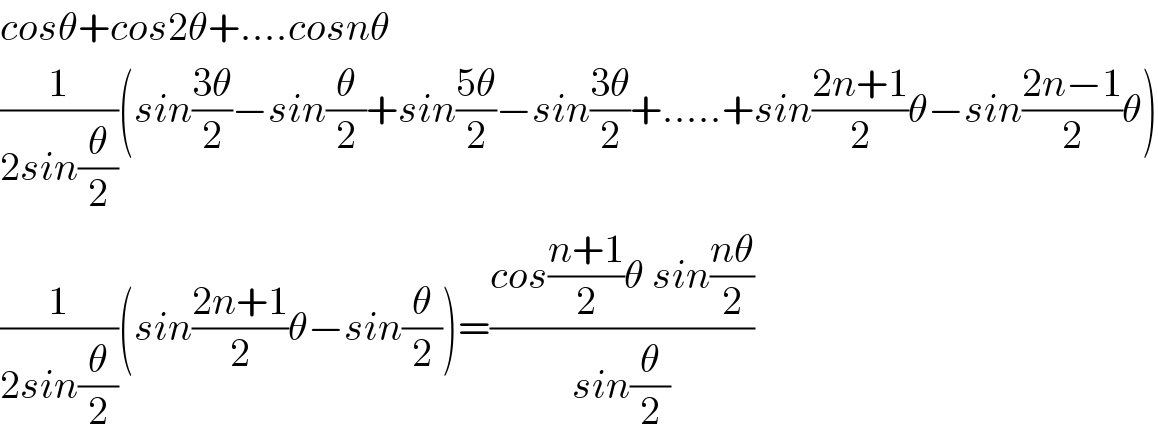
cosθ+cos2θ+....cosnθ (1/(2sin(θ/2)))(sin((3θ)/2)−sin(θ/2)+sin((5θ)/2)−sin((3θ)/2)+.....+sin((2n+1)/2)θ−sin((2n−1)/2)θ) (1/(2sin(θ/2)))(sin((2n+1)/2)θ−sin(θ/2))=((cos((n+1)/2)θ sin((nθ)/2))/(sin(θ/2)))
$${cos}\theta+{cos}\mathrm{2}\theta+….{cosn}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}\left({sin}\frac{\mathrm{3}\theta}{\mathrm{2}}−{sin}\frac{\theta}{\mathrm{2}}+{sin}\frac{\mathrm{5}\theta}{\mathrm{2}}−{sin}\frac{\mathrm{3}\theta}{\mathrm{2}}+…..+{sin}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\theta−{sin}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\theta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}\left({sin}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\theta−{sin}\frac{\theta}{\mathrm{2}}\right)=\frac{{cos}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta\:{sin}\frac{{n}\theta}{\mathrm{2}}}{{sin}\frac{\theta}{\mathrm{2}}} \\ $$
Answered by Dwaipayan Shikari last updated on 10/Jul/20
sinθ+sin2θ+....sin nθ (1/(2sin(θ/2)))(cos(θ/2)−cos((3θ)/2)+cos((3θ)/2)−cos((5θ)/2)+....+cos((2n−1)/2)θ−cos((2n+1)/2)θ) (1/(2sin(θ/2)))(cos(θ/2)−cos((2n+1)/2)θ) (1/(2sin(θ/2))).2sin((n+1)/2)θsin(n/2)θ =((sin((n+1)/2)θ sin(n/2)θ)/(sin(θ/2))) So sinθ+cosθ+sin2θ+cos2θ+...... n =((sin(n/2)θ)/(sin(θ/2)))(cos((n+1)/2)θ+sin((n+1)/2)θ)
$${sin}\theta+{sin}\mathrm{2}\theta+….{sin}\:{n}\theta \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}\left({cos}\frac{\theta}{\mathrm{2}}−{cos}\frac{\mathrm{3}\theta}{\mathrm{2}}+{cos}\frac{\mathrm{3}\theta}{\mathrm{2}}−{cos}\frac{\mathrm{5}\theta}{\mathrm{2}}+….+{cos}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}}\theta−{cos}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\theta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}\left({cos}\frac{\theta}{\mathrm{2}}−{cos}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}}\theta\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{sin}\frac{\theta}{\mathrm{2}}}.\mathrm{2}{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta{sin}\frac{{n}}{\mathrm{2}}\theta\:\:\:=\frac{{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta\:{sin}\frac{{n}}{\mathrm{2}}\theta}{{sin}\frac{\theta}{\mathrm{2}}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$${So}\: \\ $$$${sin}\theta+{cos}\theta+{sin}\mathrm{2}\theta+{cos}\mathrm{2}\theta+……\:\:{n} \\ $$$$ \\ $$$$=\frac{{sin}\frac{{n}}{\mathrm{2}}\theta}{{sin}\frac{\theta}{\mathrm{2}}}\left({cos}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta+{sin}\frac{{n}+\mathrm{1}}{\mathrm{2}}\theta\right) \\ $$
Answered by mathmax by abdo last updated on 10/Jul/20
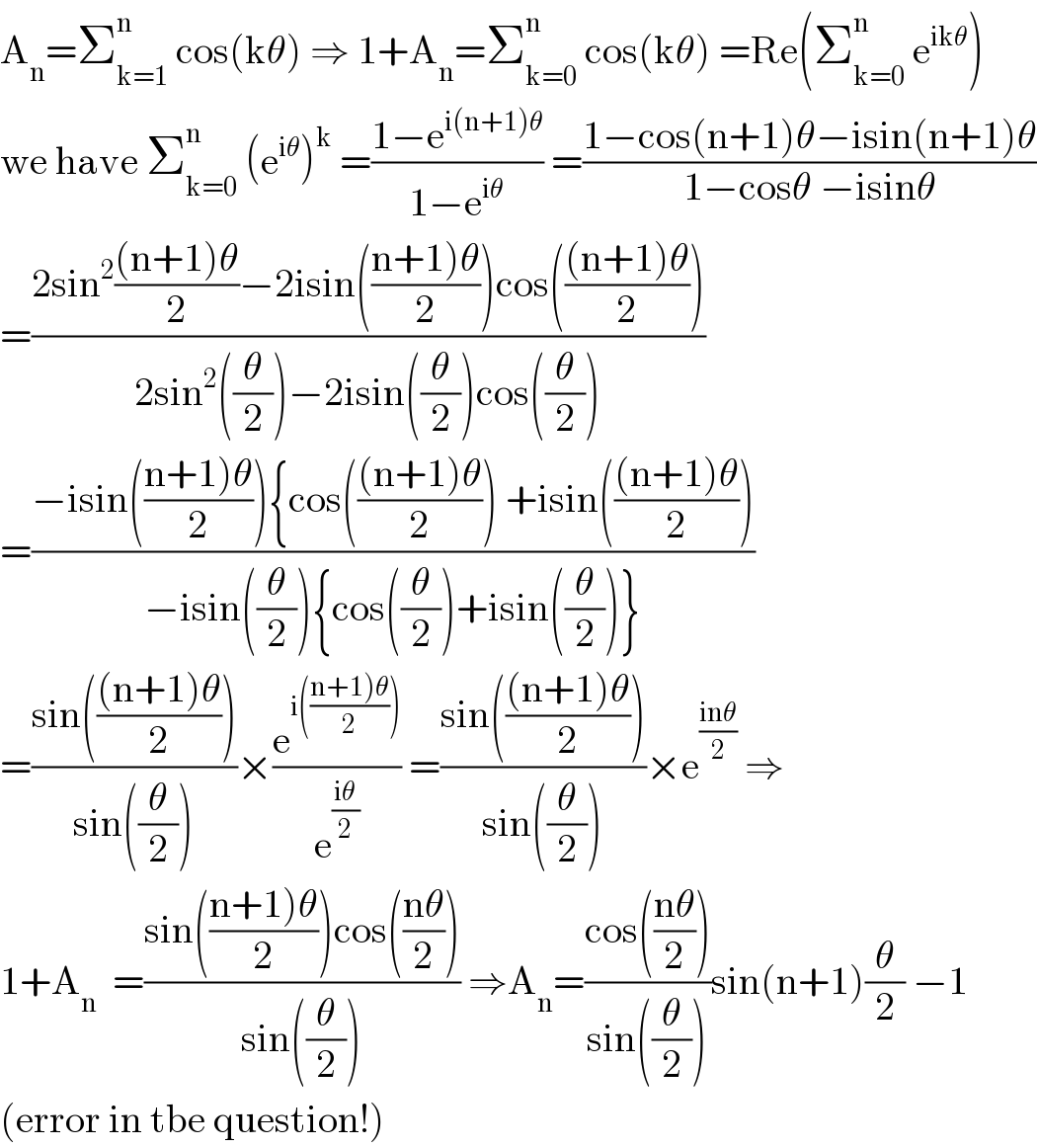
A_n =Σ_(k=1) ^n cos(kθ) ⇒ 1+A_n =Σ_(k=0) ^n cos(kθ) =Re(Σ_(k=0) ^n e^(ikθ) ) we have Σ_(k=0) ^n (e^(iθ) )^k =((1−e^(i(n+1)θ) )/(1−e^(iθ) )) =((1−cos(n+1)θ−isin(n+1)θ)/(1−cosθ −isinθ)) =((2sin^2 (((n+1)θ)/2)−2isin(((n+1)θ)/2))cos((((n+1)θ)/2)))/(2sin^2 ((θ/2))−2isin((θ/2))cos((θ/2)))) =((−isin(((n+1)θ)/2)){cos((((n+1)θ)/2)) +isin((((n+1)θ)/2)))/(−isin((θ/2)){cos((θ/2))+isin((θ/2))})) =((sin((((n+1)θ)/2)))/(sin((θ/2))))×(e^(i(((n+1)θ)/2))) /e^((iθ)/2) ) =((sin((((n+1)θ)/2)))/(sin((θ/2))))×e^((inθ)/2) ⇒ 1+A_n =((sin(((n+1)θ)/2))cos(((nθ)/2)))/(sin((θ/2)))) ⇒A_n =((cos(((nθ)/2)))/(sin((θ/2))))sin(n+1)(θ/2) −1 (error in tbe question!)
$$\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{k}\theta\right)\:\Rightarrow\:\mathrm{1}+\mathrm{A}_{\mathrm{n}} =\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{cos}\left(\mathrm{k}\theta\right)\:=\mathrm{Re}\left(\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\mathrm{e}^{\mathrm{ik}\theta} \right) \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{n}} \:\left(\mathrm{e}^{\mathrm{i}\theta} \right)^{\mathrm{k}} \:=\frac{\mathrm{1}−\mathrm{e}^{\mathrm{i}\left(\mathrm{n}+\mathrm{1}\right)\theta} }{\mathrm{1}−\mathrm{e}^{\mathrm{i}\theta} }\:=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{n}+\mathrm{1}\right)\theta−\mathrm{isin}\left(\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{1}−\mathrm{cos}\theta\:−\mathrm{isin}\theta} \\ $$$$=\frac{\mathrm{2sin}^{\mathrm{2}} \frac{\left(\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}−\mathrm{2isin}\left(\frac{\left.\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)}{\mathrm{2sin}^{\mathrm{2}} \left(\frac{\theta}{\mathrm{2}}\right)−\mathrm{2isin}\left(\frac{\theta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)} \\ $$$$=\frac{−\mathrm{isin}\left(\frac{\left.\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)\left\{\mathrm{cos}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)\:+\mathrm{isin}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)\right.}{−\mathrm{isin}\left(\frac{\theta}{\mathrm{2}}\right)\left\{\mathrm{cos}\left(\frac{\theta}{\mathrm{2}}\right)+\mathrm{isin}\left(\frac{\theta}{\mathrm{2}}\right)\right\}} \\ $$$$=\frac{\mathrm{sin}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\theta}{\mathrm{2}}\right)}×\frac{\mathrm{e}^{\mathrm{i}\left(\frac{\left.\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)} }{\mathrm{e}^{\frac{\mathrm{i}\theta}{\mathrm{2}}} }\:=\frac{\mathrm{sin}\left(\frac{\left(\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\theta}{\mathrm{2}}\right)}×\mathrm{e}^{\frac{\mathrm{in}\theta}{\mathrm{2}}} \:\Rightarrow \\ $$$$\mathrm{1}+\mathrm{A}_{\mathrm{n}} \:\:=\frac{\mathrm{sin}\left(\frac{\left.\mathrm{n}+\mathrm{1}\right)\theta}{\mathrm{2}}\right)\mathrm{cos}\left(\frac{\mathrm{n}\theta}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\theta}{\mathrm{2}}\right)}\:\Rightarrow\mathrm{A}_{\mathrm{n}} =\frac{\mathrm{cos}\left(\frac{\mathrm{n}\theta}{\mathrm{2}}\right)}{\mathrm{sin}\left(\frac{\theta}{\mathrm{2}}\right)}\mathrm{sin}\left(\mathrm{n}+\mathrm{1}\right)\frac{\theta}{\mathrm{2}}\:−\mathrm{1} \\ $$$$\left(\mathrm{error}\:\mathrm{in}\:\mathrm{tbe}\:\mathrm{question}!\right) \\ $$
Commented by Dwaipayan Shikari last updated on 10/Jul/20
yes sir . it will be sin(θ/2) instead of sin((nθ)/2) i think
$${yes}\:{sir}\:.\:{it}\:{will}\:{be}\:{sin}\frac{\theta}{\mathrm{2}}\:\:{instead}\:{of}\:{sin}\frac{{n}\theta}{\mathrm{2}}\:\:{i}\:{think} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *