Menu Close

show-that-cos-i-sin-n-cosn-i-sin-

Tinku Tara 0 Comments
Pin




Question Number 81010 by M±th+et£s last updated on 08/Feb/20
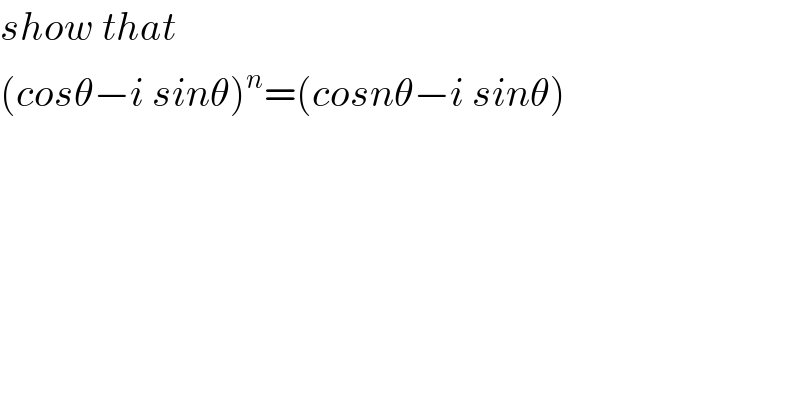
show that (cosθ−i sinθ)^n =(cosnθ−i sinθ)
$${show}\:{that} \\ $$$$\left({cos}\theta−{i}\:{sin}\theta\right)^{{n}} =\left({cosn}\theta−{i}\:{sin}\theta\right) \\ $$
Commented by MJS last updated on 08/Feb/20
wrong
$$\mathrm{wrong} \\ $$
Commented by M±th+et£s last updated on 08/Feb/20
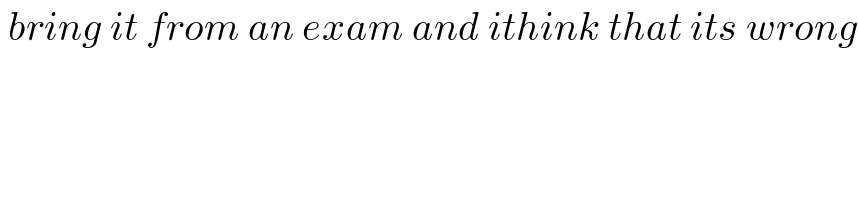
bring it from an exam and ithink that its wrong
$$\:{bring}\:{it}\:{from}\:{an}\:{exam}\:{and}\:{ithink}\:{that}\:{its}\:{wrong} \\ $$
Commented by MJS last updated on 08/Feb/20
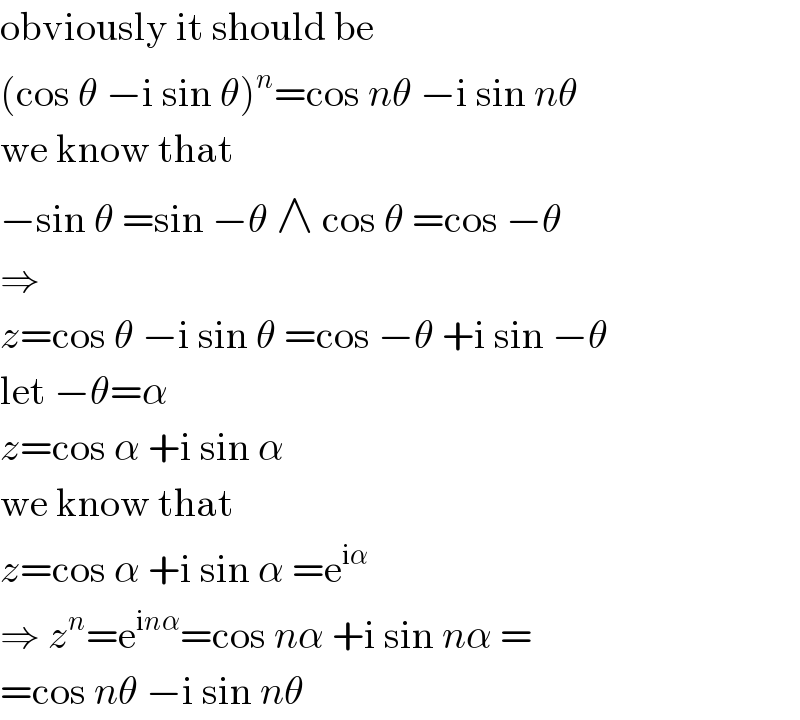
obviously it should be (cos θ −i sin θ)^n =cos nθ −i sin nθ we know that −sin θ =sin −θ ∧ cos θ =cos −θ ⇒ z=cos θ −i sin θ =cos −θ +i sin −θ let −θ=α z=cos α +i sin α we know that z=cos α +i sin α =e^(iα) ⇒ z^n =e^(inα) =cos nα +i sin nα = =cos nθ −i sin nθ
$$\mathrm{obviously}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be} \\ $$$$\left(\mathrm{cos}\:\theta\:−\mathrm{i}\:\mathrm{sin}\:\theta\right)^{{n}} =\mathrm{cos}\:{n}\theta\:−\mathrm{i}\:\mathrm{sin}\:{n}\theta \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that} \\ $$$$−\mathrm{sin}\:\theta\:=\mathrm{sin}\:−\theta\:\wedge\:\mathrm{cos}\:\theta\:=\mathrm{cos}\:−\theta \\ $$$$\Rightarrow \\ $$$${z}=\mathrm{cos}\:\theta\:−\mathrm{i}\:\mathrm{sin}\:\theta\:=\mathrm{cos}\:−\theta\:+\mathrm{i}\:\mathrm{sin}\:−\theta \\ $$$$\mathrm{let}\:−\theta=\alpha \\ $$$${z}=\mathrm{cos}\:\alpha\:+\mathrm{i}\:\mathrm{sin}\:\alpha \\ $$$$\mathrm{we}\:\mathrm{know}\:\mathrm{that} \\ $$$${z}=\mathrm{cos}\:\alpha\:+\mathrm{i}\:\mathrm{sin}\:\alpha\:=\mathrm{e}^{\mathrm{i}\alpha} \\ $$$$\Rightarrow\:{z}^{{n}} =\mathrm{e}^{\mathrm{i}{n}\alpha} =\mathrm{cos}\:{n}\alpha\:+\mathrm{i}\:\mathrm{sin}\:{n}\alpha\:= \\ $$$$=\mathrm{cos}\:{n}\theta\:−\mathrm{i}\:\mathrm{sin}\:{n}\theta \\ $$
Commented by abdomathmax last updated on 09/Feb/20
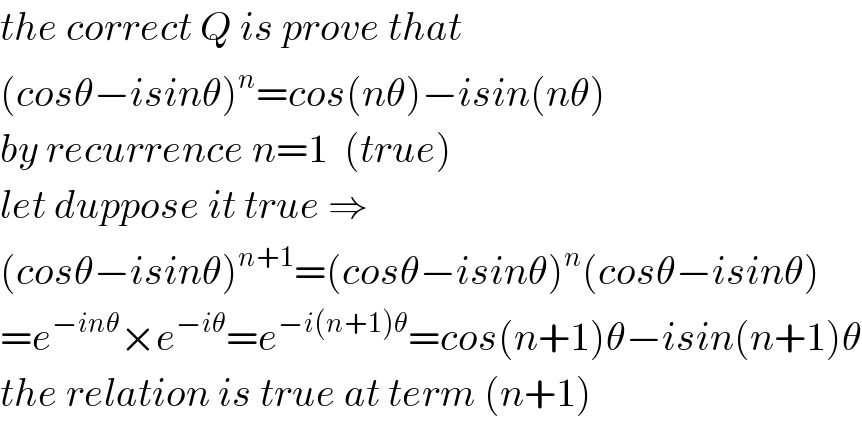
the correct Q is prove that (cosθ−isinθ)^n =cos(nθ)−isin(nθ) by recurrence n=1 (true) let duppose it true ⇒ (cosθ−isinθ)^(n+1) =(cosθ−isinθ)^n (cosθ−isinθ) =e^(−inθ) ×e^(−iθ) =e^(−i(n+1)θ) =cos(n+1)θ−isin(n+1)θ the relation is true at term (n+1)
$${the}\:{correct}\:{Q}\:{is}\:{prove}\:{that} \\ $$$$\left({cos}\theta−{isin}\theta\right)^{{n}} ={cos}\left({n}\theta\right)−{isin}\left({n}\theta\right) \\ $$$${by}\:{recurrence}\:{n}=\mathrm{1}\:\:\left({true}\right) \\ $$$${let}\:{duppose}\:{it}\:{true}\:\Rightarrow \\ $$$$\left({cos}\theta−{isin}\theta\right)^{{n}+\mathrm{1}} =\left({cos}\theta−{isin}\theta\right)^{{n}} \left({cos}\theta−{isin}\theta\right) \\ $$$$={e}^{−{in}\theta} ×{e}^{−{i}\theta} ={e}^{−{i}\left({n}+\mathrm{1}\right)\theta} ={cos}\left({n}+\mathrm{1}\right)\theta−{isin}\left({n}+\mathrm{1}\right)\theta \\ $$$${the}\:{relation}\:{is}\:{true}\:{at}\:{term}\:\left({n}+\mathrm{1}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *