Menu Close

show-that-derivative-of-Sin-x-x-1-

Tinku Tara 0 Comments
Pin




Question Number 150180 by jlewis last updated on 10/Aug/21
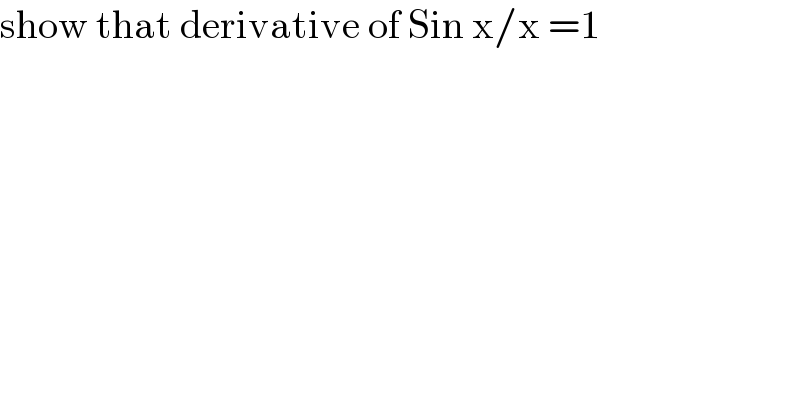
show that derivative of Sin x/x =1
$$\mathrm{show}\:\mathrm{that}\:\mathrm{derivative}\:\mathrm{of}\:\mathrm{Sin}\:\mathrm{x}/\mathrm{x}\:=\mathrm{1} \\ $$$$ \\ $$
Answered by liberty last updated on 10/Aug/21
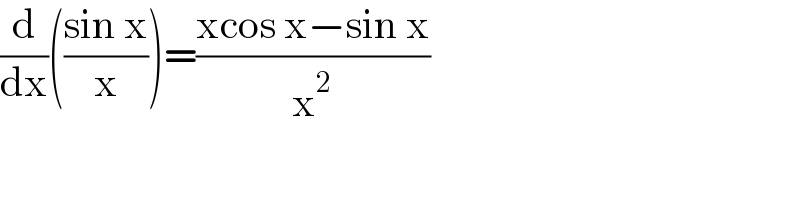
(d/dx)(((sin x)/x))=((xcos x−sin x)/x^2 )
$$\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}\right)=\frac{\mathrm{xcos}\:\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }\: \\ $$
Commented by liberty last updated on 10/Aug/21
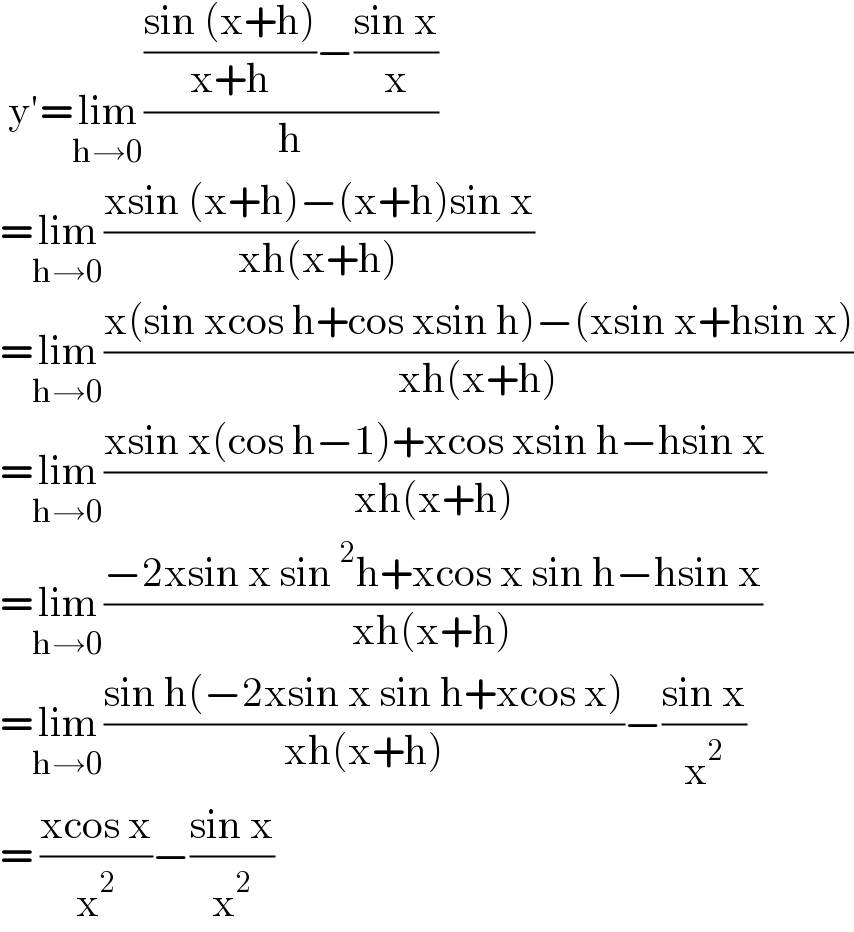
y′=lim_(h→0) ((((sin (x+h))/(x+h))−((sin x)/x))/h) =lim_(h→0) ((xsin (x+h)−(x+h)sin x)/(xh(x+h))) =lim_(h→0) ((x(sin xcos h+cos xsin h)−(xsin x+hsin x))/(xh(x+h))) =lim_(h→0) ((xsin x(cos h−1)+xcos xsin h−hsin x)/(xh(x+h))) =lim_(h→0) ((−2xsin x sin^2 h+xcos x sin h−hsin x)/(xh(x+h))) =lim_(h→0) ((sin h(−2xsin x sin h+xcos x))/(xh(x+h)))−((sin x)/x^2 ) = ((xcos x)/x^2 )−((sin x)/x^2 )
$$\:\mathrm{y}'=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{sin}\:\left(\mathrm{x}+\mathrm{h}\right)}{\mathrm{x}+\mathrm{h}}−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}}}{\mathrm{h}} \\ $$$$=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{xsin}\:\left(\mathrm{x}+\mathrm{h}\right)−\left(\mathrm{x}+\mathrm{h}\right)\mathrm{sin}\:\mathrm{x}}{\mathrm{xh}\left(\mathrm{x}+\mathrm{h}\right)} \\ $$$$=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}\left(\mathrm{sin}\:\mathrm{xcos}\:\mathrm{h}+\mathrm{cos}\:\mathrm{xsin}\:\mathrm{h}\right)−\left(\mathrm{xsin}\:\mathrm{x}+\mathrm{hsin}\:\mathrm{x}\right)}{\mathrm{xh}\left(\mathrm{x}+\mathrm{h}\right)} \\ $$$$=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{xsin}\:\mathrm{x}\left(\mathrm{cos}\:\mathrm{h}−\mathrm{1}\right)+\mathrm{xcos}\:\mathrm{xsin}\:\mathrm{h}−\mathrm{hsin}\:\mathrm{x}}{\mathrm{xh}\left(\mathrm{x}+\mathrm{h}\right)} \\ $$$$=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{2xsin}\:\mathrm{x}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{h}+\mathrm{xcos}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{h}−\mathrm{hsin}\:\mathrm{x}}{\mathrm{xh}\left(\mathrm{x}+\mathrm{h}\right)} \\ $$$$=\underset{\mathrm{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{sin}\:\mathrm{h}\left(−\mathrm{2xsin}\:\mathrm{x}\:\mathrm{sin}\:\mathrm{h}+\mathrm{xcos}\:\mathrm{x}\right)}{\mathrm{xh}\left(\mathrm{x}+\mathrm{h}\right)}−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\:\frac{\mathrm{xcos}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{2}} } \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *